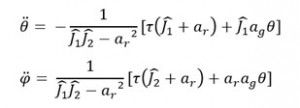Robot DiWheel 2021
Bonjour à toutes et à tous
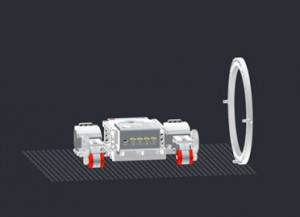
Nous sommes heureux de vous présenter notre projet, le robot DiWheel. Notre robot se base sur une structure de LEGO, mais beaucoup de travail technique a été nécessaire pour mener ce passionnant projet à bien.
Si cela vous intéresse, n’hésitez pas, et cliquez sur ce lien pour en savoir plus !
-> Lire l’article complet <-
Robot DiWheel 2021
Étudiant à Polytech Angers nous avons eu, Adrien Soubrane et Corentin Amoruso, la chance de travailler sur l’un des projets proposés au cours de notre dernier semestre. Notre choix s’est porté sur l’étude du robot DiWheel !
Un DiWheel est un véhicule avec deux grandes roues latérales. Il a été inventé en 1880 mais n’a pas conquis le grand public, ce qui l’a fait disparaitre.
En effet, les balancements sont le principal défaut de ce moyen de transport.
L’objectif a été de concevoir un prototype de A à Z à l’aide du kit LEGO Mindstorm EV3 mais aussi d’étudier la stabilité de ce dernier.
Ce travail est une partie très importante car il permet de modéliser le robot, à la manière d’une maquette, avant de pouvoir le répliquer à échelle humaine.
C’est donc un projet sur la durée, et nous espérons sincèrement qu’un grand modèle verra le jour à Polytech Agers, grâce (en partie) à nos travaux.
Le contrôle du robot doit se faire en Bluetooth, dans notre cas avec une application smartphone.
Ce projet est très complet : nous avons dû, d’ans l’ordre, concevoir le robot, le contrôler, illustrer son comportement via des capteurs, modéliser mathématiquement le système, et mettre en place une loi de commande, pour réguler les oscillations.
Exemple de modélisation sous Studio 2.0
Nous devons réduire au maximum les oscillations, et nous devons y penser dès la création de la structure.
Nous avons donc choisi de placer la brique EV3 non pas au niveau de l’axe des roues mais en dessous. Cela permet d’abaisser le centre de gravité, en le plaçant sous l’axe des roues.
Pour la conception des roues, le choix de l’imprimante 3D était intéressant, mais trop contraignant, surtout avec le confinement. Nous avons donc décidé d’utiliser des quarts de roues LEGO. Nous n’avions plus qu’à trouver un moyen de les fixer à l’EV3.
Arc de roue dentée
Roue du robot
Mécanisme côté gauche
L’étape suivante du projet a été de trouver une nouvelle manière de contrôler le DiWheel. En effet, ce dernier ne dispose que d’un seul moyen pour cela : appuyer directement sur les boutons de la brique EV3. C’est pourquoi nous voulions trouver un moyen plus amusant et pratique pour faire avancer notre robot. C’est de cette réflexion qu’ont découlées les idées de contrôler le DiWheel à l’aide d’une manette et d’une application.
A la manière d’un Mario Kart, nous voulions pouvoir maîtriser notre robot à l’aide d’une Wiimote et du gyroscope intégré.
Pour cela, nous voulions nous servir de la communication Bluetooth commune à l’EV3 et à la manette. Il fallait donc trouver un moyen de programmer la Wiimote afin de communiquer avec la brique EV3. La solution la plus simple est d’utiliser GlovePIE. C’est un logiciel dédié pour la Wiimote permettant de l’utiliser avec n’importe quel périphérique.
Malheureusement, compte tenu des conditions de travail (confinement, matériel, problème de Bluetooth…) nous n’avons pas pu connecter les deux périphériques ensembles. Néanmoins la solution reste viable si BlueSoleil ou un autre pilote fonctionne sur l’ordinateur utilisé pour la manipulation.
Une autre solution existe : modifier le système d’exploitation de la brique pour utiliser un programme disponible sur internet. Mais cette dernière nous semblait trop risquée, nous ne voulions pas endommager l’EV3.
Manette WiiMote
Source: https://nintendo-museum.fr/wii-wheel/
Cependant, grâce à RemotEV3, une application android, nous pouvons commander le robot via bluetooth.
Le robot peut ainsi être dirigé dans toutes les directions et tous les sens.
La connexion étant plus simple avec un smartphone, nous n’avons eu aucun souci de fonctionnement.
Voici quelques démonstrations en vidéo :
Elle se déroule en trois parties : l’étude du système, la représentation d’état et l’expérimentation.
L’étude du système consiste à déterminer l’ensemble des constantes, des forces et des vitesses appliquées au robot afin de déterminer un modèle théorique. Il servira pour déterminer une représentation d’état contenant les variables que nous voulons changer. C’est pourquoi il ne faut pas perdre de vue notre but : réduire les balancements.
Notre choix s’est donc porté sur le modèle Lagrangien nous permettant d’obtenir les formules de l’accélération angulaire des roues et du corps. En effet, en atténuant les variations d’accélération, le robot deviendra plus stable.
Après simplification nous avons obtenus les formules respectives de l’accélération du corps et celle des roues :
Équations de Lagrange
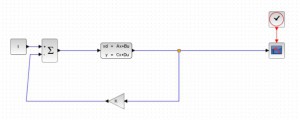
Une fois que nous avons obtenu nos formules, on s’est intéressé à la représentation d’état. Grâce à cette loi de commande on peut comprendre de manière théorique comment évoluent nos variables.
Une représentation d’état est composée d’une entrée X, d’une sortie Y et de différentes matrices (A, B, C et D) montrant l’évolution du système.
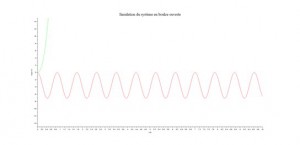
A l’aide de Scilab, nous avons confirmé théoriquement l’instabilité du système. En effet, après avoir reproduit virtuellement le système à l’aide de la représentation d’état, nous avons simulé et obtenu la courbe correspondant à l’angle du corps par rapport à l’axe y. Cette dernière forme une sinusoïde caractéristique d’une instabilité (ici des balancements). Certes les valeurs et le comportement obtenu sont cohérents, néanmoins pour pouvoir les utiliser il faut vérifier expérimentalement si cela concorde avec la réalité.
courbe modélisation (sinusoïdale)
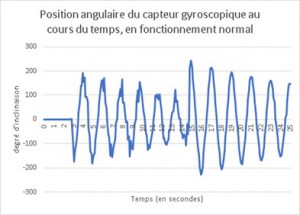
Avec le logiciel (Windows) LEGO Mindstorm EV3 et grâce aux capteurs gyroscopiques et l’accéléromètre fournis dans le kit, nous avons pu prendre quelques mesures. En comparant les valeurs obtenues avec les capteurs et celles de la simulation, nous avons pu confirmer que notre modèle est utilisable pour la commande du système.
Courbe gyroscope (robot instable)
positionnement des capteurs
Enfin, commander le système :
Exemple de simulation sous Scilab
Bilan :
Ce projet a été pour nous une occasion de nous amuser et de travailler plus en profondeur sur des notions complexes. Il nous a permis de développer nos compétences dans différents domaines (Physique, mathématique, automatisme, conception…).
Nous avons aussi appris à travailler en équipe, en autonomie et à surmonter les difficultés à l’aide de nos connaissances, et grâce à nos recherches.
Même si le projet n’a pas abouti au niveau de la commande par retour d’état, nous sommes fiers d’avoir obtenu un DiWheel fonctionnel et commandable via smartphone.
Ressources :
Le projet touchant à sa fin, il nous tenait à cœur de pouvoir vous donner la possibilité de continuer ce dernier. En effet, si vous disposez vous aussi du kit LEGO Mindstorm EV3 et que vous souhaitez reproduire et améliorer notre robot, nous mettons à votre disposition l’ensemble des étapes de construction :
Compte rendu et instructions de montage
Ce drive contient également notre compte rendu de projet, que nous vous incitons vivement à consulter si vous souhaitez reproduire un robot du même style.
Pour plus de question, n’hésitez pas à nous contacter via nos adresses mail respectives :
Merci pour votre lecture ! A très vite !
Corentin & Adrien
Bonjour à toutes et à tous,
Nous sommes Théo TROUILLARD et Adrien FRAT, deux étudiants en deuxième année de cycle préparatoire à Polytech Angers. Lors du semestre quatre de notre formation, nous avons réalisé un projet de conception qui avait pour intitulé “Modélisation mathématique et simulation numérique de la phyllotaxie”. Lors de ce projet, nos professeurs référents ont été Madame Laetitia PEREZ et Monsieur Laurent AUTRIQUE.
Le mot phyllotaxie vient du grec et il désigne l’arrangement des feuilles ou des fruits d’un être végétal. Ces arrangements sont multiples et ce phénomène permet donc une grande diversité des végétaux dans la nature. En effet, il existe différents types de phyllotaxie et chacun est caractérisé par le nombre de feuilles par nœud d’une plante et par l’angle de divergence entre ces feuilles.
Par exemple, sur cette photo de camérisier à balais, on voit très bien qu’il y a deux feuilles par noeud et que ces deux feuilles sont séparées par un angle de divergence de 180° :
Image 1 : Photo de camérisier à balais
L’objectif de ce projet était de proposer une ou plusieurs simulations de ces arrangements à l’aide d’un outil informatique afin de simuler le développement de certaines plantes.
Notre projet s’est divisé en quatre grandes étapes.
D’abord, une phase de documentation où nous avons pu appréhender le sujet en nous renseignant grâce à différents supports sur ce qu’était la phyllotaxie.
Puis, il y a eu une phase d’étude. Dans cette phase, nous nous sommes intéressés plus particulièrement aux différents types de phyllotaxie et à leurs modèles mathématiques, c’est-à-dire à la façon dont on pouvait définir chaque type de phyllotaxie. Nous avons identifié cinq types principaux de phyllotaxie :
Ensuite est venu le moment de réaliser nos simulations. Pour cela, nous avons utilisé le logiciel Scilab. Nous avons retenu seulement quatre types de phyllotaxie (les quatre premières citées précédemment).
Enfin, la dernière phase de notre projet concernait la rédaction de notre rapport.
Comme dit précédemment, avant de mettre en œuvre les simulations sur Scilab, nous avons d’abord étudié les modèles mathématiques. Pour nous aider, nous avons réalisé des schémas pour chaque type de phyllotaxie. Pendant notre étude, nous avons vu que nous avions la possibilité de travailler avec des coordonnées polaires car chaque point est défini selon un angle et une distance au centre.
Image 2 : Schéma représentant la phyllotaxie alternée distique
Image 3 : Schéma représentant la phyllotaxie opposée décussée
A partir de ces schémas, nous avons essayé de déterminer des algorithmes pour chaque cas de phyllotaxie. Puis, nous avons adapté ces algorithmes pour les retranscrire dans Scilab.
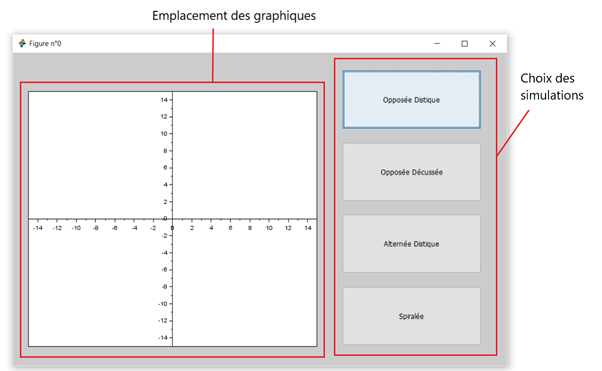
Ainsi, nous avons réalisé 4 simulations différentes (exemple dans le prochain paragraphe) que nous avons réunies à l’aide d’une interface graphique.
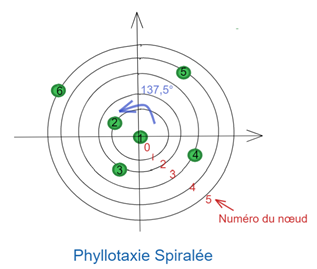
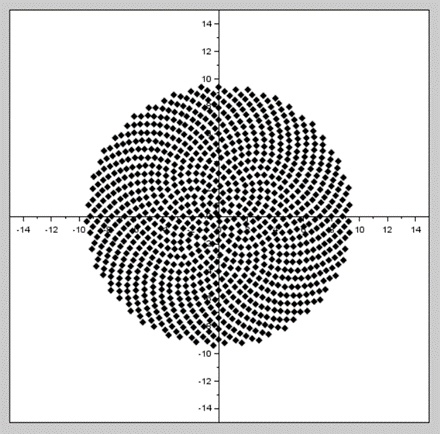
Prenons comme exemple la phyllotaxie spiralée (rappel : une feuille par nœud, deux feuilles successives séparées par un angle de divergence de 137,5°) dont voici le schéma que nous avons fait :
Image 4 : Schéma représentant la phyllotaxie spiralée
On voit que pour chaque feuille (une feuille étant représentée par un point vert) l’angle va évoluer et la distance au centre va augmenter. On va donc raisonner avec une boucle itérative.
On commence par initialiser un incrément à 0 (Exemple: n = 0)
Puis commence notre boucle qui va de n au nombre d’itérations souhaité.
Enfin, on termine la boucle en augmentant l’incrément (n+1).
On peut retranscrire cet algorithme sous Scilab en ajoutant dans la boucle l’affichage de chaque point sur un graphique.
Nous obtenons le résultat graphique suivant :
Image 5 : Résultat graphique de notre simulation pour la phyllotaxie spiralée
Nous avons donc réussi à établir quatre simulations différentes que nous avons réunies dans une interface graphique avec Scilab. Pour cela, nous avons utilisé le module GUI Builder de Scilab. Nous sommes fiers du résultat final mais nous sommes conscients qu’il peut être amélioré (ajout de couleurs, simulation en 3D,…). De plus, ce projet nous a permis de réinvestir et/ou d’acquérir de nouvelles connaissances et de travailler en groupe, ce qui est un aspect important du métier d’ingénieur..
Image 6 : Aperçu de notre interface graphique
——————————————————————————————————————-
Image 1 : image prise sur un blog botanique (http://www.annie-claude-bolomier.fr)
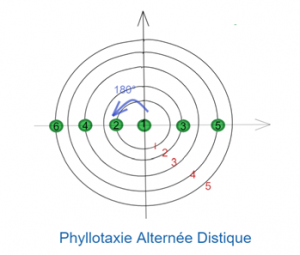
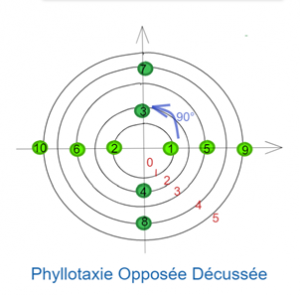
Image 2,3 et 4 : schémas réalisés avec le logiciel draw.u-angers.fr
Image 5 et 6 : obtenues avec nos codes Scilab