Bonjour à toutes et à tous,
Nous sommes Théo TROUILLARD et Adrien FRAT, deux étudiants en deuxième année de cycle préparatoire à Polytech Angers. Lors du semestre quatre de notre formation, nous avons réalisé un projet de conception qui avait pour intitulé “Modélisation mathématique et simulation numérique de la phyllotaxie”. Lors de ce projet, nos professeurs référents ont été Madame Laetitia PEREZ et Monsieur Laurent AUTRIQUE.
Le mot phyllotaxie vient du grec et il désigne l’arrangement des feuilles ou des fruits d’un être végétal. Ces arrangements sont multiples et ce phénomène permet donc une grande diversité des végétaux dans la nature. En effet, il existe différents types de phyllotaxie et chacun est caractérisé par le nombre de feuilles par nœud d’une plante et par l’angle de divergence entre ces feuilles.
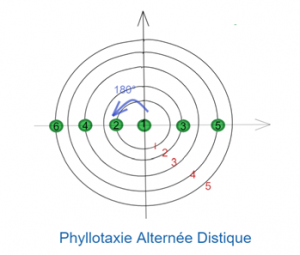
Par exemple, sur cette photo de camérisier à balais, on voit très bien qu’il y a deux feuilles par noeud et que ces deux feuilles sont séparées par un angle de divergence de 180° :
Image 1 : Photo de camérisier à balais
L’objectif de ce projet était de proposer une ou plusieurs simulations de ces arrangements à l’aide d’un outil informatique afin de simuler le développement de certaines plantes.
Notre projet s’est divisé en quatre grandes étapes.
D’abord, une phase de documentation où nous avons pu appréhender le sujet en nous renseignant grâce à différents supports sur ce qu’était la phyllotaxie.
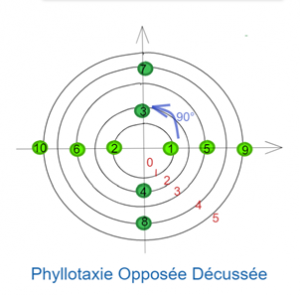
Puis, il y a eu une phase d’étude. Dans cette phase, nous nous sommes intéressés plus particulièrement aux différents types de phyllotaxie et à leurs modèles mathématiques, c’est-à-dire à la façon dont on pouvait définir chaque type de phyllotaxie. Nous avons identifié cinq types principaux de phyllotaxie :
Ensuite est venu le moment de réaliser nos simulations. Pour cela, nous avons utilisé le logiciel Scilab. Nous avons retenu seulement quatre types de phyllotaxie (les quatre premières citées précédemment).
Enfin, la dernière phase de notre projet concernait la rédaction de notre rapport.
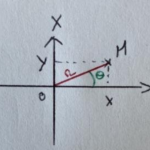
Comme dit précédemment, avant de mettre en œuvre les simulations sur Scilab, nous avons d’abord étudié les modèles mathématiques. Pour nous aider, nous avons réalisé des schémas pour chaque type de phyllotaxie. Pendant notre étude, nous avons vu que nous avions la possibilité de travailler avec des coordonnées polaires car chaque point est défini selon un angle et une distance au centre.
Image 2 : Schéma représentant la phyllotaxie alternée distique
Image 3 : Schéma représentant la phyllotaxie opposée décussée
A partir de ces schémas, nous avons essayé de déterminer des algorithmes pour chaque cas de phyllotaxie. Puis, nous avons adapté ces algorithmes pour les retranscrire dans Scilab.
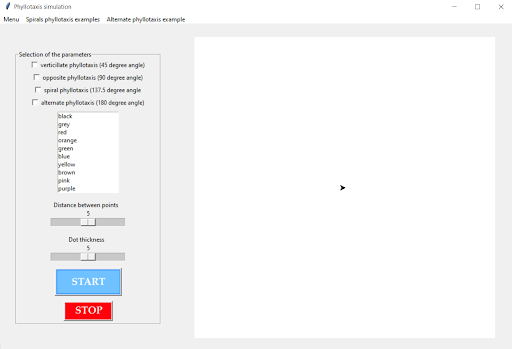
Ainsi, nous avons réalisé 4 simulations différentes (exemple dans le prochain paragraphe) que nous avons réunies à l’aide d’une interface graphique.
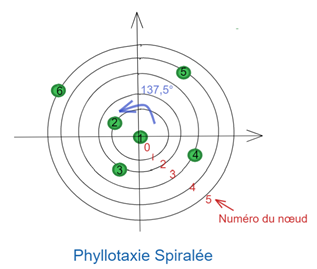
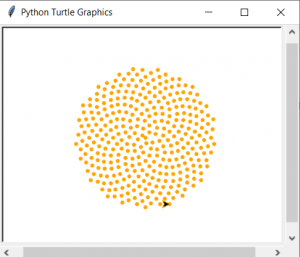
Prenons comme exemple la phyllotaxie spiralée (rappel : une feuille par nœud, deux feuilles successives séparées par un angle de divergence de 137,5°) dont voici le schéma que nous avons fait :
Image 4 : Schéma représentant la phyllotaxie spiralée
On voit que pour chaque feuille (une feuille étant représentée par un point vert) l’angle va évoluer et la distance au centre va augmenter. On va donc raisonner avec une boucle itérative.
On commence par initialiser un incrément à 0 (Exemple: n = 0)
Puis commence notre boucle qui va de n au nombre d’itérations souhaité.
Enfin, on termine la boucle en augmentant l’incrément (n+1).
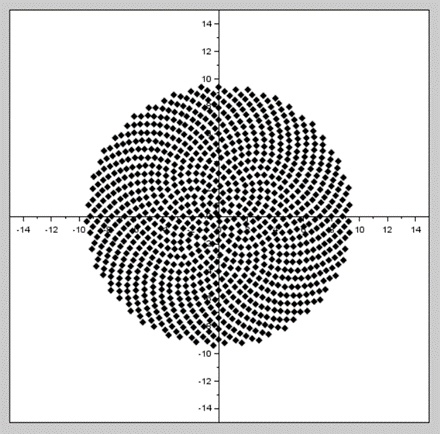
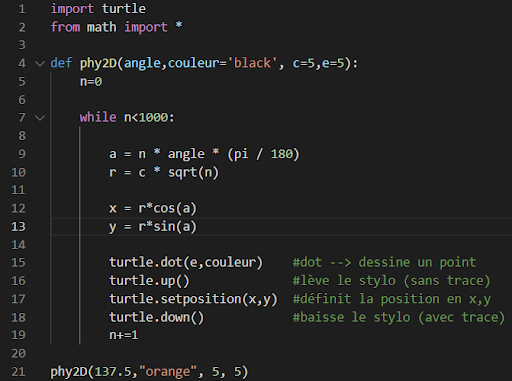
On peut retranscrire cet algorithme sous Scilab en ajoutant dans la boucle l’affichage de chaque point sur un graphique.
Nous obtenons le résultat graphique suivant :
Image 5 : Résultat graphique de notre simulation pour la phyllotaxie spiralée
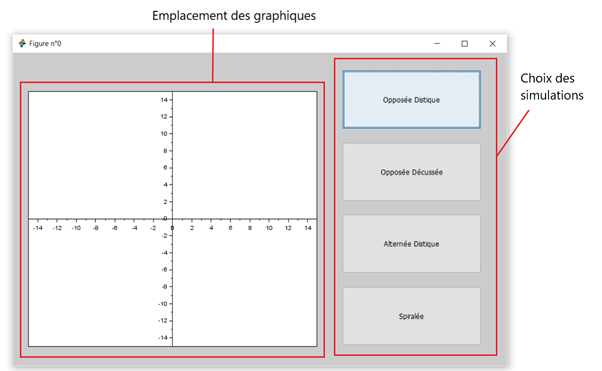
Nous avons donc réussi à établir quatre simulations différentes que nous avons réunies dans une interface graphique avec Scilab. Pour cela, nous avons utilisé le module GUI Builder de Scilab. Nous sommes fiers du résultat final mais nous sommes conscients qu’il peut être amélioré (ajout de couleurs, simulation en 3D,…). De plus, ce projet nous a permis de réinvestir et/ou d’acquérir de nouvelles connaissances et de travailler en groupe, ce qui est un aspect important du métier d’ingénieur..
Image 6 : Aperçu de notre interface graphique
——————————————————————————————————————-
Image 1 : image prise sur un blog botanique (http://www.annie-claude-bolomier.fr)
Image 2,3 et 4 : schémas réalisés avec le logiciel draw.u-angers.fr
Image 5 et 6 : obtenues avec nos codes Scilab
