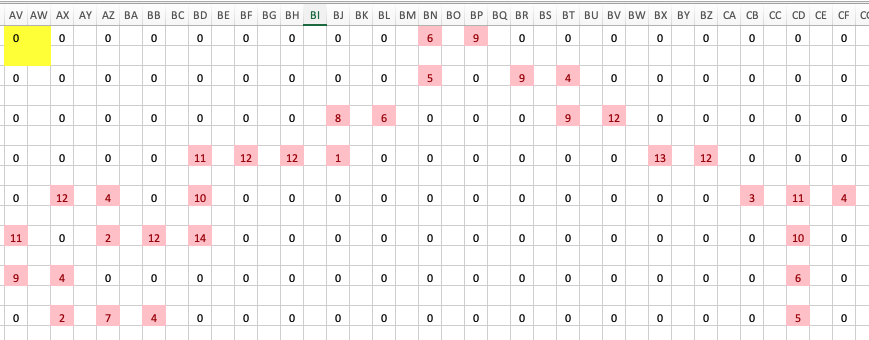
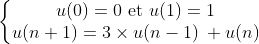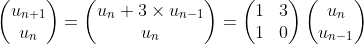J’ai eu l’occasion de faire plusieurs vidéos de montres originales sur ma chaine Youtube, en particulier :
- Créer des montres Tokyoflash (Python sur NUMWORKS)
- JavaScript & SVG – Montre RADIOACTIVE
- JavaScript & SVG – Simulation de la montre STENCIL TokyoFlash
- JavaScript – Simulation de la montre TENMETSU de TokyoFlash
- JavaScript – Simulation de montres TokyoFlash
Aujourd’hui nous allons nous inspirer des horloges ALBERT qui ne vous donnent l’heure qu’après avoir effectué un calcul arithmétique (additions, soustractions, multiplications ou divisions suivant le niveau choisi)
Je vous propose différentes versions web inspirées par cette idée. Une fois les fichiers récupérés, vous n’aurez besoin d’aucune connexion Internet et vous pourrez mettre les fichiers sur une tablette ou un ordinateur portable.
Installation et modifications
Par défaut les horloges s’actualisent toutes les 60 secondes. Pour modifier cet intervalle, ouvrez le fichier .html avec le bloc-note puis rechercher la ligne contenant 60000 (60 millisecondes). Remplacez cette valeur par exemple par 20000 (pour 20 secondes) et enregistrez.
Concernant les tablettes, mettre le 2 fichiers (.html et .ttf) sur votre tablette (via Bluetooth, par mail ou autre), par exemple dans le dossier download ou documents. Pour ouvrir le fichier .html avec un navigateur installé sur votre tablette (Chrome ou FireFox ou Brave), lancez le navigateur puis tapez l’adresse (avec 3 « / ») :
file:///storage/emulated/0/download/horloge.html
ou
file:///storage/emulated/0/documents/horloge.htmlSi les fichiers sont sur une carte SD, l’adresse sera du type :
file:///sdcard/download/horloge.htmlUne fois que vous avez réussi, mettre la page en Favori. Si vous n’y arrivez pas, vous pouvez toujours utiliser les liens démo ci-dessous, mais il vous faudra alors une connexion Internet.
Additions et soustractions
Téléchargez | Voir la démo en ligne
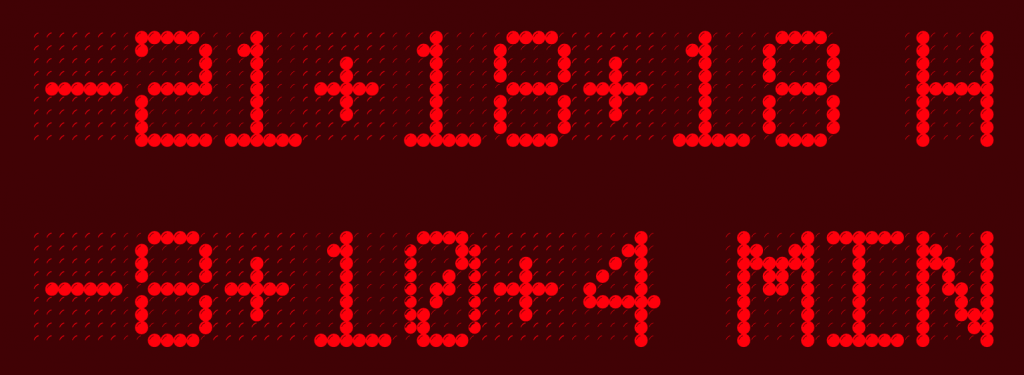
Pour créer la formule des heures, l’idée a été de choisir au hasard 2 nombres entre -24 et 24 (par exemple -21 et +18), de les additionner (-3) et de regarder si la différence entre l’heure actuelle (par exemple 15h) et cette somme est ou non entre -24 et 24. Ici 15 – (-3) = 18 convient. D’où la formule -21+18+18. Sinon, on tire à nouveau 2 entiers et on recommence, les ordinateurs étant rapides, on ne se rend pas compte s’il y a eu besoin de 1 ou 1000 essais !
Addition et multiplication
Téléchargez | Voir la démo en ligne
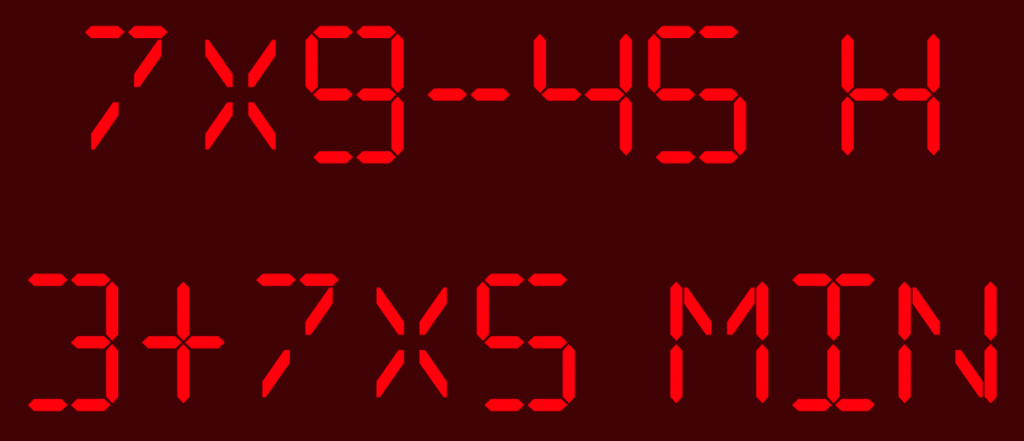
Les 2 nombres à multiplier sont choisis entre 2 et 9, l’un des 2 pouvant être négatif. Le troisième nombre est calculé pour obtenir le bon résultat (la bonne heure puis même chose avec les minutes). Volontairement les 2 lignes n’ont pas le même ordre d’affichage : a×b+c pour les heures et a+b×c pour les minutes.
Version points sur des dés
Téléchargez | Voir la démo en ligne

C’est en regardant un manuel de CP cycle 2 que j’ai eu l’idée de cette version. Le programme est assez simple, on compte les dizaines et les unités (un dé existe pour tous les chiffres entre 0 et 9). Lorsque l’on a un multiple de 10, on s’arrange pour n’afficher que les dés « 10 » (qui est en fait le caractère « = »). Il n’y a qu’avec « 0 » seul que l’on affiche le dé sans point.
AFF = n => n == 0 ? // n vaut 0 ?
0 : // si oui on renvoie 0
'='.repeat(0 | n / 10) // Nombre de dizaines
+ (n % 10 != 0 ? n % 10 : '') // et unités si pas 0Version aiguilles : Heures – Minutes – Secondes
Téléchargez | Voir la démo en ligne | Version tirage aléatoire de l’heure

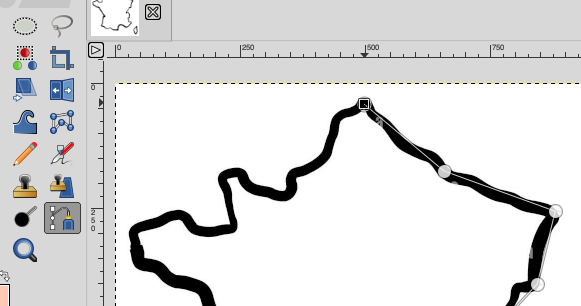
L’horloge provient de Wikipedia, elle est au format SVG (donc transformable sans perte de qualité). Modification du SVG avec Inkscape pour créer les 2 visuels (heures et minutes), il a suffit ensuite de donner les noms heures, minutes, secondes aux aiguilles et d’appliquer une rotation en JavaScript (en précisant dans Inkscape où est le centre de rotation) :
var hm = HM(new Date().toLocaleTimeString())
// h[0] contient l'heure, h[1] les minutes et h[2] les secondes
heures.setAttribute('transform','rotate('+(hm[0]*30)+')');
minutes.setAttribute('transform','rotate('+(hm[1]*6)+')');
secondes.setAttribute('transform','rotate('+(hm[2]*6)+')');Version cercle trigonométrique
Téléchargez | Voir la démo en ligne

La formule pour les minutes n’est qu’une fonction affine : 0 min est à 90° et 60 min à -270°. On obtient la formule :
ANGLEMIN = min => -6 * min + 90On fait ensuite un test pour savoir si le nombre est plus petit que -180 (par exemple -246), si c’est le cas on affichera plutôt -246 + 360 = 114°
La stratégie est la même pour les heures, en faisant attention aux 2 cas : heures entre 3h et 9h puis entre 9h-12h-3h. La formule utilisée est :
ANGLEH = h => -30 * (h % 12) + 90 // le % correspond à 'modulo'Système d’équations
Téléchargez | Voir la démo en ligne

Pour ne pas avoir de nombres trop grands, les coefficients devant les heures sont choisis aléatoirement entre -4 et 4 (et non nuls), et entre -3 et 3 pour les minutes (non nuls).
Il faut aussi s’arranger pour ne pas afficher les coefficients 1 et -1 (par exemple 1H s’écrit H et -1M s’écrit -M), pour cela on peut écrire cette fonction :
UN = n => Math.abs(n) != 1 ? n : n == 1 ? '' : '-'
>> UN(5)
5
>> UN(1)
''
>> UN(-1)
'-'Version binaire
Téléchargez | Voir la démo en ligne

Le programme est encore plus simple puisqu’en JavaScript on transforme un nombre en binaire par :
>> (15).toString(2)
'1111'
>> (30).toString(2)
'11110'Pour écrire les heures nous avons besoin d’au plus 5 bits et 6 bits pour les minutes.
>> BIN = (n, s) => ('0'.repeat(5) + n.toString(2)).slice(-s)
>> BIN(15,5) // 15 écrit sur 5 bits
'01111'
>> BIN(30,6) // 30 écrit sur 6 bits
'011110'Version binaire plus simple
Téléchargez | Voir la démo en ligne
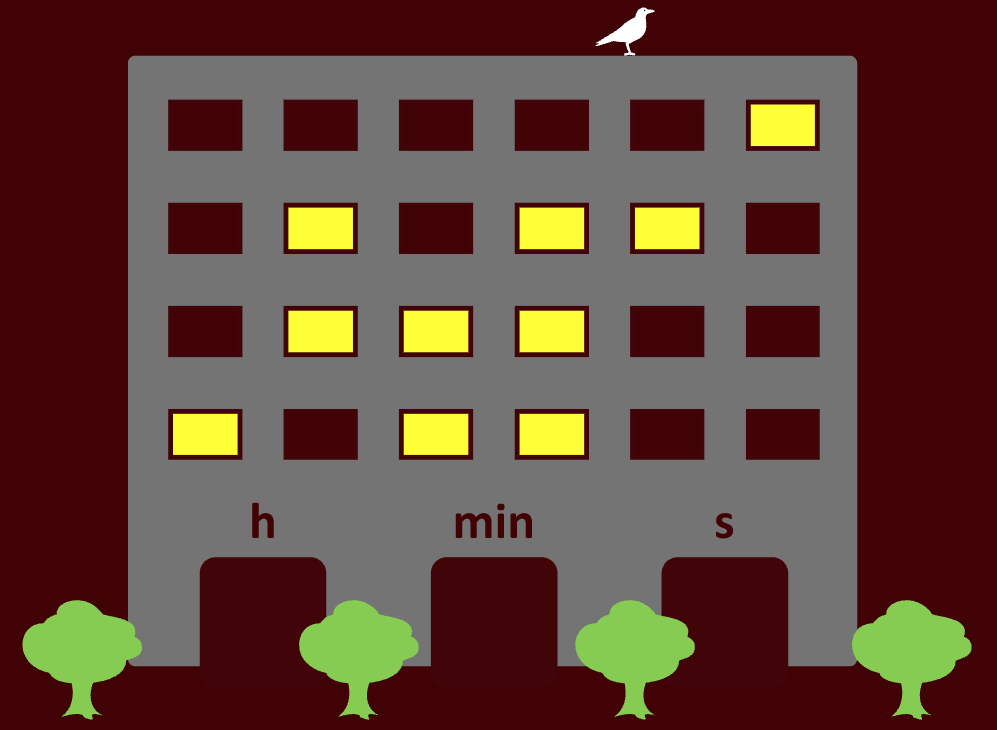
Une colonne se lit de bas en haut et les fenêtres valent 1, 2, 4 et 8
Dizaine pour les heures = 1, Unités pour les heures = 2 + 4 = 6
Dizaine pour les minutes = 1 + 2 = 3, Unités pour les minutes = 1 + 2 + 4 = 7
Dizaines pour les secondes = 4, Unités pour les secondes = 8
Il est 16 h 37 min 48 s
Une vraie horloge existe, elle se nomme « The City Clock » et vous la trouverez ici.
Le dessin a été réalisé avec Inkscape, les fenêtres ont été nommées hd1, hd2…, hu1, hu2,… pour les dizaines et unités des heures, idem avec les md, mu et sd, su.
Exemple avec 16 h : On récupère la dizaine (1) et l’unité (6) que l’on transforme en binaire (1 et 110). On parcourt les 4 fenêtres de la colonne dizaine et on met en jaune s’il y a un « 1 » sinon marron. Donc avec « 1 » seule la fenêtre du bas sera allumée. Avec 6, on parcourt les 4 fenêtres de la colonne unité et on allume la 2e et 3e fenêtre.
BIN = n => [...'0'.repeat(3)+n.toString(2)].reverse().join('')
>> BIN(6)
'011000'
>> BIN(1)
'1000'
ETAT = (v, col) => { // Exemple v = 6 et col = 'hu'
b = BIN(v) // Transformation du chiffre en binaire
for (let i = 0; i < 4; i++) { // 4 fenêtres par colonne
c = document.getElementById(col+(i+1)) // La fenêtre
c.setAttribute('fill', b[i] == '0' ? '#490101' : 'yellow');
}
}
>> ETAT(6, 'hu') va allumer ou éteindre la colonne "heure unités" pour afficher 6Version hexadécimale (pour les designers)
Téléchargez | Voir la démo en ligne

La notation utilisée est celle que l’on trouve pour le codage des couleurs (retouche d’images, HTML…), par exemple le rouge vif correspond à #FF0000. Le programme est quasi identique à la version binaire :
>> HEX = n => ('0' + n.toString(16)).slice(-2).toUpperCase()
>> HEX(14)
'0E'
>> HEX(42)
'2A'
>> HEX(20)
'14'Inversement, pour décoder, il faut prendre l’unité (entre 0 et F) et ajouter 16 fois la dizaine.
Horloge de Fibonacci
Téléchargez | Voir la démo en ligne

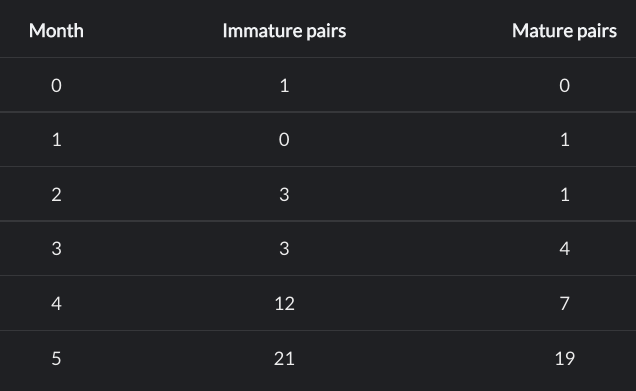
La suite de Fibonacci est : 0,1,1,2,3,5,8,13,21,34,55,89… où le terme suivant est la somme des 2 précédents.
Théorème de Zeckendorf : Tous les entiers peuvent s’écrire comme une somme de nombres de Fibonacci.
// Liste des nombres de Fibonacci qui seront utiles
>> F = [0,1,1,2,3,5,8,13,21,34,55]
// Décomposition de n en somme
>> FIBO = n => {
res = [ ] // Résultat final
while (n > 0) { // Tant que n n'est pas nul
// On cherche le plus grand nb de Fibonacci inférieur à n
a = F.filter(v => v <= n).slice(-1)[0]
// On l'ajoute au tableau
res.push(F.indexOf(a))
// n diminue du nombre trouvé
n -= a
}
return res // On retourne le résultat
}
>> FIBO(13)
[7] // 13 = F(7)
>> FIBO(44)
[9, 6, 3] // 44 = F(9)+F(6)+F(3)
>> FIBO(51)
(4) [9, 7, 4, 1] // 51 = F(9)+F(7)+F(4)+F(1)Horloge romaine
Téléchargez | Voir la démo en ligne
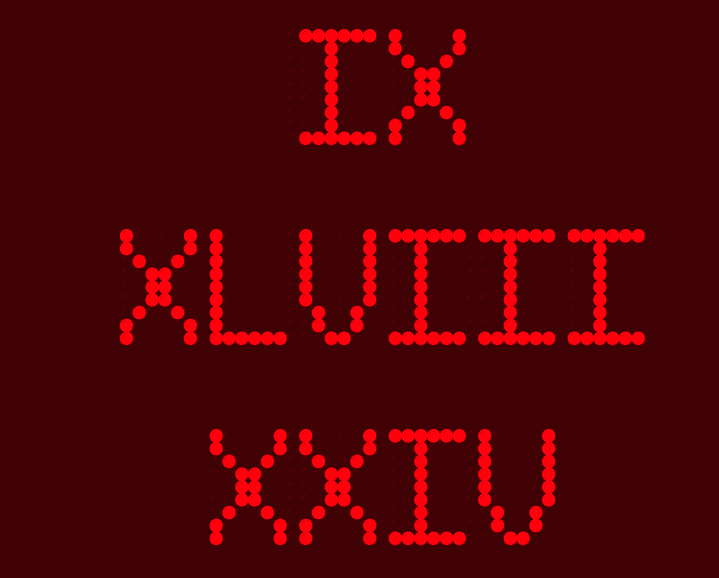
On trouve facilement sur Internet un algorithme pour convertir un nombre en numérotation romaine :
var arabe = [1000,900,500,400,100,90,50,40,10,9,5,4,1]
var romain = 'M,CM,D,CD,C,XC,L,XL,X,IX,V,IV,I'.split(',')
var CONV = nb => {
if (nb == 0) return ' '
var s = ''
for (i in arabe) {
var q = 0 | nb / arabe[i]; // division entière
var nb = nb % arabe[i] // reste de la division
s += romain[i].repeat(q)
}
return s
}
>> CONV(9)
'IX'
>> CONV(48)
'XLVIII'
>> CONV(24)
'XXIV'
Exemple du déroulement de l’algorithme pour 47 (Div = Division):
Reste = 47
Div du reste par 1000 = 0, reste = 47, ajout 0 =
Div du reste par 900 = 0, reste = 47, ajout 0 =
Div du reste par 500 = 0, reste = 47, ajout 0 =
Div du reste par 400 = 0, reste = 47, ajout 0 =
Div du reste par 100 = 0, reste = 47, ajout 0 =
Div du reste par 90 = 0, reste = 47, ajout 0 =
Div du reste par 50 = 0, reste = 47, ajout 0 =
Div du reste par 40 = 1, reste = 7, ajout 40 = XL // 40*1
Div du reste par 10 = 0, reste = 7, ajout 0 = XL
Div du reste par 9 = 0, reste = 7, ajout 0 = XL
Div du reste par 5 = 1, reste = 2, ajout 5 = XLV // 5*1
Div du reste par 4 = 0, reste = 2, ajout 0 = XLV
Div du reste par 1 = 2, reste = 0, ajout 2 = XLVII // 1*2Pour ne pas voir les secondes, utilisez ce code :
setInterval(function x() {
var hm = HM(new Date().toLocaleTimeString())
document.querySelector("#hr").innerHTML = CONV(hm[0])
document.querySelector("#mn").innerHTML = CONV(hm[1])
return x
}(), 60000);et supprimez la ligne :
<div id='se'></div> Horloge « IL RESTE »
Téléchargez (changement toutes les 30 secondes) | Voir la démo (changement toutes les 4 secondes)

C’est le même programme que addition et soustraction, il suffit de remplacer l’heure par IL RESTE et de trouver un calcul qui donnera le nombre 60 – minutes