Produit externe
Le produit externe sert à composer chacun des termes de l’opérande gauche avec chacun des termes de l’opérande droit par n’importe quelle fonction dyadique.
L’exemple classique est la table de multiplication de Pythagore :
1 2 3 ∘.× 1 2 3 4 5 ⍝ ∘ se prononce JOT Output: 1 2 3 4 5 2 4 6 8 10 3 6 9 12 15 ⍴ 1 2 3 ∘.× 1 2 3 4 5 Output: 3 5 ⍝ 3 lignes et 5 colonnes
Chacune des valeurs du vecteur 1 2 3 est multipliée par chacune des valeurs du vecteur 1 2 3 4 5.
On peut obtenir un résultat analogue en RPL de plusieurs façons :
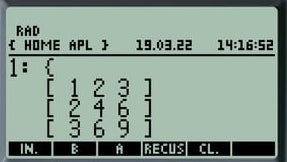
1: [ 1 2 3 ] # Sous forme de matrice
2: { 1 2 3 4 5 } # Sous forme de liste
×
1: {[1 2 3] [2 4 6] [3 6 9] [4 8 12] [5 10 15]}
Ou encore, en inversant matrice et liste :
1: { 1 2 3 } # Sous forme de liste
2: [ 1 2 3 4 5 ] # Sous forme de matrice
×
1: {[1 2 3 4 5] [2 4 6 8 10] [3 6 9 12 15]}
Cela fonctionne également avec la division d’une matrice par une liste (pas l’inverse) :
En APL :
1 2 3 4 5 ∘.÷ 1 2 3
Output:
1 0.5 0.3333333333
2 1 0.6666666667
3 1.5 1
4 2 1.333333333
5 2.5 1.666666667
En RPL :
1: [ 1 2 3 4 5] # Matrice
2: { 1 2 3 } # Liste
÷
1: {[1 2 3 4 5]
[.5 1 1.5 2 2.5]
[.333 .666 1 1.333 1.666]
}
Voici la version proposée par Norman Brenner pour le produit externe X ∘. Y où X et Y peuvent être des vecteurs ou des matrices. Nous appellerons PE. le produit externe :
« → x y f « y « x f EVAL » MAP » » 'PE. STO
Exemple avec la table de multiplication :
3: [ 1 2 3 ] # ou { 1 2 3 }
2: [ 1 2 3 4 5 ] # ou { 1 2 3 4 5 }
1: « × »
VAR PE.
1: ⌈ 1 2 3 4 5 ⌉
| 2 4 6 8 10 |
⌊ 3 6 9 12 15 ⌋
Le principe : On prend un par un les éléments de y (ici y = [1 2 3 4 5]) et on multiplie la valeur par la matrice x (ici x = [1 2 3]). Ce qui permet d’obtenir les colonnes [1 2 3] puis [2 4 6] etc. Mais si l’on veut faire une table d’addition, le script proposé fera 1 + [1 2 3] ce qui va renvoyer une erreur. Par contre, avec les listes on peut faire 1 ADD {1 2 3} pour obtenir la liste {2 3 4} (le “+” étant réservé à la concaténation)
Table d’addition en utilisant des listes :
3: { 1 2 3 }
2: { 1 2 3 4 5 }
1: « ADD »
VAR PE.
1: {{2 3 4 5 6} {3 4 5 6 7} {4 5 6 7 8}}
On peut inventer des tables de Pythagore généralisées, par exemple la table des maximums :
5 4 8 ∘.⌈ 7 3 9 1 Output: 7 5 9 5 7 4 9 4 8 8 9 8
En RPL :
3: { 5 4 8 }
2: { 7 3 9 1 }
1: « MAX »
VAR PE.
1: {{7 5 9 5} {7 4 9 4} {8 8 9 8}}
La première ligne correspond aux max entre 5 et les valeurs 7 3 9 1
La seconde ligne aux max entre 4 et 7 3 9 1
Et la dernière ligne aux max entre 8 et 7 3 9 1
Exemple – Répartition des âges
On se donne une liste d’âges et une liste de répartitions, par exemple on veut savoir combien de personnes ont entre 10 et 15 ans, entre 15 ans et 40 ans et plus de 40 ans.
AGES ← 27 12 18 75 40 22 35 6 ⍝ Les âges TRAN ← 10 15 40 ⍝ Tranches d'âges TRAN ∘.< AGES ⍝ Matrice des comparaisons 1 1 1 1 1 1 1 0 1 0 1 1 1 1 1 0 0 0 0 1 0 0 0 0 CUM ← +/ TRAN ∘.< AGES ⍝ Cumul des lignes 7 6 1
7 personnes ont plus de 10 ans, 6 ont plus de 15 ans et 1 a plus de 40 ans. Pour obtenir le nombre de personnes par intervalle :
CUM - 1↓CUM,0 ⍝ Différence entre les termes 1 5 1
1 personne a entre 10 et 15 ans, 5 personnes entre 15 et 40 ans et 1 personne a plus de 40 ans. L’enfant de 6 ans a bien été éliminé de nos statistiques.
En RPL :
3 : { 10 15 40 }
2 : { 27 12 18 75 40 22 35 6 }
1: « < »
VAR PE.
1: {{1 1 1 1 1 1 1 0}
{1 0 1 1 1 1 1 0}
{0 0 0 1 0 0 0 0}}
1: « ∑LIST »
PGR LIST PROC DOLIST
1: { 7 6 1 }
La fonction △LIST transforme {x1, x2, … xn} en {x2-x1, … xn-xn-1}, or nous voulons {x1-x2, … xn-1 -xn, xn}. On va donc ajouter un 0 à la liste, utiliser △LIST et prendre la valeur absolue (on pourrait aussi inverser la liste, ajouter un 0 en première position puis △LIST et à nouveau inverser la liste…).
1: { 7 6 1 }
0 + △LIST ABS
1: {1 5 1}
Résumons cela sous la forme d’un programme STAT, en APL :
STAT ← {c - 1↓(c ← +/⍺ ∘.< ⍵),0}
TRAN STAT AGES
Output:
1 5 1
Et en RPL :
« « < » PE. « ∑LIST » DOLIST
0 + △LIST ABS
»
'STA STO
3 : { 10 15 40 }
2 : { 27 12 18 75 40 22 35 6 }
VAR STAT
1: { 1 5 1 }
Exercice – Années bissextiles
Définition (Wikipédia) : Pour être bissextile, une année doit dans tous les cas être divisible par 4 ; mais si c’est une année de centenaire (comme 1800, 1900, etc.), elle doit en complément être divisible par 400.
Voici une version en APL trouvée sur le site APLcart et légèrement modifiée pour ne faire apparaitre que les années :
BIS ← {(0 ≠.= 400 100 4 ∘.| ⍵) / ⍵}
BIS 1900 2000 1908 2022 2024
Output:
2000 1908 2024
On reconnait le produit externe ∘.|, le produit interne ≠.= et la compression logique /. Voici l’idée du programme :
400 100 4 ∘.| ⍵ : On cherche les restes des divisions des années par 400, 100 et 4. Ce qui fait une matrice de 3 lignes :
400 100 4 ∘.| 1900 2000 1908 2022 2024 Output: 300 0 308 22 24 ⍝ Restes des divisions par 400 0 0 8 22 24 ⍝ Restes des divisions par 100 0 0 0 2 0 ⍝ Restes des divisions par 4
0 ≠.= : Rappelez-vous de +.× qui signifie “somme des produits”, ou “faire les produits puis réduire par la somme”. Ici on doit donc effectuer les tests 0 = “termes de la matrice” puis réduire par ≠… Essayons de comprendre :
0 = 400 100 4 ∘.| 1900 2000 1908 2022 2024 Output: 0 1 0 0 0 1 1 0 0 0 1 1 1 0 1
Un “1” dans cette nouvelle matrice indique que la division tombe juste.
Voici maintenant l’astuce utilisée : Si vous regardez les 8 cas a priori possibles pour une année donnée, à savoir être ou non divisible par 400 (noté DIV 400. plus loin), être ou non divisible par 100 et être ou non divisible par 4, certains cas sont impossibles (par exemple être divisible par 400 mais pas par 4, etc.). Il ne reste que 4 possibilités :
DIV 4. DIV 100. DIV 400. BISSEXTILE ?
F F F NON
V F F OUI
V V F NON
V V V OUI
Effectuons maintenant les réductions de chacune des lignes en utilisant ≠ :
(F ≠ F) ≠ F <=> F ≠ F <=> F (V ≠ F) ≠ F <=> V ≠ F <=> V (V ≠ V) ≠ F <=> F ≠ F <=> F (V ≠ V) ≠ V <=> F ≠ V <=> V
Donc le produit interne 0 ≠.= indiquera bien si l’année est bissextile ou pas ! Je vous laisse 3 exemples à méditer :
0 = 400 100 4 ∘.| 1900 Output: 0 1 1 ≠/ 0 = 400 100 4 ∘.| 1900 Output: 0 0 = 400 100 4 ∘.| 2024 Output: 0 0 1 ≠/ 0 = 400 100 4 ∘.| 2024 Output: 1 0 = 400 100 4 ∘.| 2022 Output: 0 0 0 ≠/ 0 = 400 100 4 ∘.| 2022 Output: 0
Il peut aussi être intéressant de remarquer qu’avec les booléens X ≠ Y est équivalent à X XOR Y (OU exclusif)
Passons à la traduction en RPL, en remarquant que MOD fonctionne entre un nombre et une liste :
2: 2024
1: {4 100 400}
MTH REAL MOD
1: {0 24 24}
De plus, comme il n’y a que 3 termes pour la réduction, on peut écrire simplement ≠ ≠. Par exemple pour (V ≠ F) ≠ F :
3: 0 # FAUX 2: 0 # FAUX 1: 1 # VRAI ≠ 2: 0 # FAUX 1: 1 # VRAI ≠ 1: 1 # VRAI
Et le test 0 = “Restes de divisions par 4, 100 et 400” est simplement le NOT en RPL (si le reste est 0, NOT donnera 1 et si le reste n’est pas nul, NOT donnera 0). D’où cette version fonctionnant avec une seule année en paramètre :
« { 4 100 400 } MOD NOT OBJ→ DROP ≠ ≠ »
'BIS STO
OBJ→ met les éléments de la liste sur la pile en ajoutant au niveau 1 la taille de la liste (que l’on supprime avec DROP).
Vérifions :
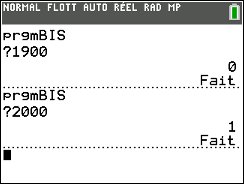
1900 VAR BIS 0 # 1900 n'est pas bissextile 2000 BIS 1 # Bissextile 2024 BIS 1 # Bissextile 2022 BIS 0 # Pas bissextile
On peut aussi écrire le programme de la façon suivante :
« { 4 100 400 } MOD NOT « ≠ » STREAM »
'BIS STO
Pour extraire les années bissextiles d’une liste, on peut par exemple faire :
« DUP « BIS » MAP SWAP IFT »
'BISL STO
1: { 1900 2000 1908 2022 2024 }
VAR BISL
{ 2000 1908 2024 }
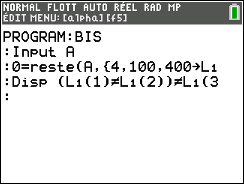
Traduction pour les Texas Instrument graphiques (TI-81, 82, 83, 84…) :