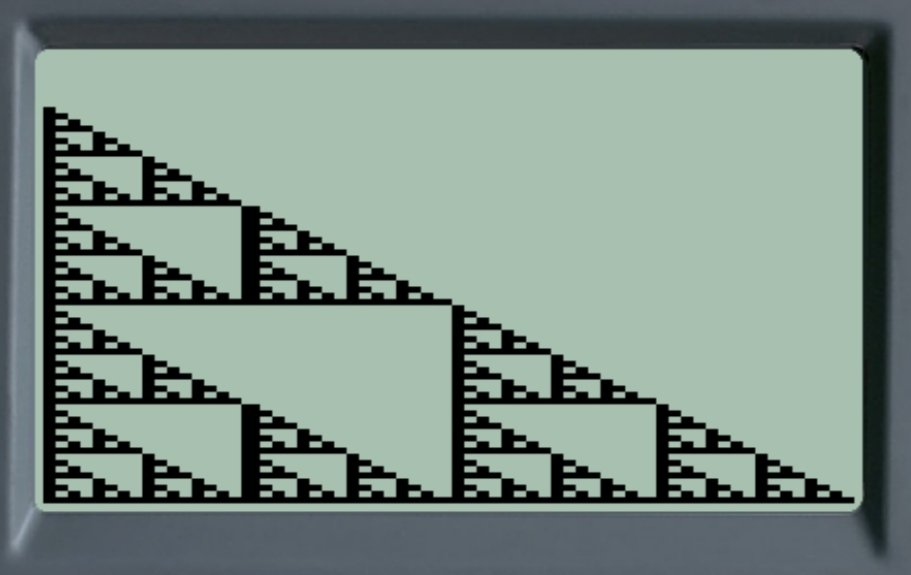
David, un collègue enseignant, a posté un tweet sur l’utilisation du mode de représentation Truth sur les anciennes calculatrices HP 48G. Voici son premier résultat, le tapis de Sierpinski :
Avec cette équation très courte :
Quelques explications : R→B permet de convertir un nombre en binaire. Pour chaque abscisse X (entre 0 et 63) et chaque Y (entre 0 et 63), on regarde s’ils ont au moins un bit en commun dans leurs écritures binaires respectives. Par exemple si X = 12 = 1100b et Y = 6 = 110b ont un bit en commun à la 3e position, on affiche dans ce cas un pixel noir à l’écran.
A partir de là j’ai trouvé la page Binary Plot du site Wollfram avec quelques visuels que j’ai voulu reproduire en Python.
from kandinsky import *
for y in range(30):
n = 2 ** y
for x in range(160):
for i in range(3):
if x ** (i + 1) & n > 0:
fill_rect(2 * x, 214 - 63 * i - 4 * y, 2, 4, (0, 0, 0))En Python il est très simple de faire des opérations bit à bit. Pour le « ET » on utilise &. Par exemple :
Pour le « OU » le symbole est |. Par exemple 12 | 6 = 14 car 1100b | 110b = 1110b
Et le « OU EXCLUSIF » par ^. Par exemple 12 ^ 6 = 10 car 1100b ^110b = 1010b
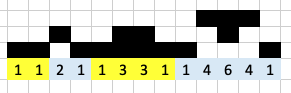
Passons à la représentation des coefficients binomiaux :
Les scripts (bibliothèque PIL et NUMWORKS) sont ici.
En bas à gauche les coefficients (écrits en binaires) qui apparaissent dans les développements de (a+b)^0, (a+b)^1, (a+b)^3 etc.
Quelques formes amusantes apparaissent !
On peut également représenter la suite de Fibonacci :
Enfin, l’idée m’est venue de représenter la conjecture de Syracuse (on part d’un entier, s’il est pair on le divise par 2 sinon on le multiplie par 3 et on ajoute 1, la conjecture prétend que l’on arrivera à 1 au bout d’un certain temps). Avec N = 27 comme départ on arrive à 1 au bout de 111 itérations (appelé temps de vol) et le maximum atteint est 9232.
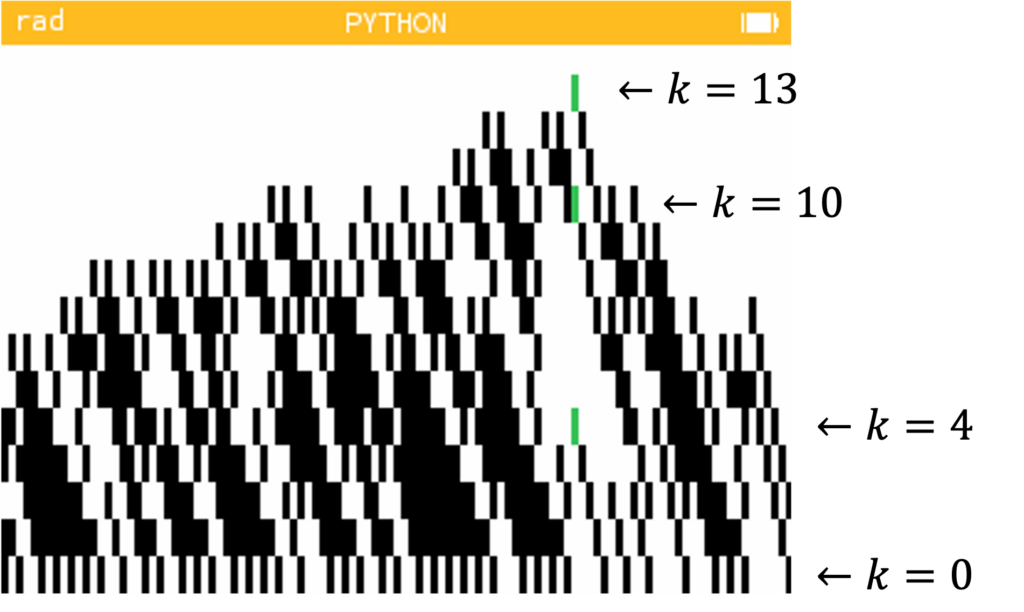
Représentons les termes de la suite sous forme binaire :
Il est alors assez facile de lire la valeur exacte de chacune des colonnes, par exemple du maximum. Il suffit de repérer les numéros de lignes (En bas = 0). Sur le visuel on lit les lignes 4, 10 et 13. Le nombre correspondant est donc 2^4 + 2^10 + 2^13 = 9232.
Autres exemples
Script NUMWORKS pour les « spirales »
from kandinsky import *
def tapis(x, y):
while x > 0 and y > 0:
if x % 3 == 1 and y % 3 == 1: return 0
x //= 3
y //= 3
return 1
for y in range(222):
for x in range(320):
if tapis(x, y): set_pixel(x, 221 - y, (0,) * 3)@ Adaptation d'un script de David Cobac pour HP-48
« 3 PICK 3 MOD » 'MOD3 STO
« 3 / IP SWAP » 'IP3 STO
{ (0 0) (130 63) X 0 (0 0) TRUTH Y } 'PPAR STO
« X Y
WHILE DUP2 *
MOD3 MOD3 *
1 ≠ *
REPEAT
IP3 IP3
END
* NOT » 'EQ STO
« ERASE DRAW {} PVIEW » 'TAP STO
Lancez TAP
Version 2 :
« X Y
WHILE DUP2 DUP2
3 MOD SWAP 3 MOD
* 1 ≠ * *
REPEAT
3 / IP SWAP 3 / IP
END
* NOT »