pascaline | Polytech Angers

Nous sommes un groupe de quatre étudiants, en 2ème année du cycle préparatoire, à l’ISTIA (Institut des Sciences et Techniques de l’Ingénieur d’Angers) ayant pris part, dans le cadre de nos études à un projet tutoré. Ce dernier a pour but de mettre en pratique nos compétences et de développer nos capacités à travailler en équipe. Dans le panel de sujets proposés, un en particulier a retenu notre attention : la Pascaline. Cet article a pour objectif d’exposer et de partager les différentes étapes par lesquelles nous sommes passés pendant la réalisation de notre projet. Blaise Pascal (1623-1662), célèbre philosophe, scientifique et théologien du 17^ème siècle, a, en son temps, révolutionné les méthodes de calcul, via l’invention de plusieurs machines à calculer, appelées : « Pascalines ». En effet, à cette époque, le calcul se pratique à l’écrit ou bien grâce à la disposition de multiples jetons, d’où dérivent les divers bouliers.Les machines à calculer de Blaise Pascal vont alors introduire une nouvelle méthode de calcul, automatique et éliminant les possibles erreurs de comptage : le calcul mécanique. Les Pascalines, capables d’effectuer des additions et des soustractions, garantissaient ainsi des calculs simplifiés et sans risque d’erreur, ce qui représentait une innovation sans précédent pour le siècle des lumières. Néanmoins ces dernières n’ont pas rencontré un franc succès et il faudra attendre le 20^ème siècle avant que ces appareils ne soient diffusés et utilisés par la plupart des caissiers. Notre projet avait donc pour but d’étudier le mécanisme des Pascalines puis , à terme, de réaliser notre propre modèle du genre. La première étape fut donc la compréhension du système permettant aux Pascalines d’effectuer des calculs. Tout d’abord, une Pascaline est en réalité composée de plusieurs « blocs ». (source: https://upload.wikimedia.org/wikipedia/commons/3/3d/Pascaline_-_top_view_and_mechanism.jpg).

Chacun de ces « blocs » possède un arbre reliant une roue d’entrée, permettant la sélection d’un chiffre, à un rouleau affichant des chiffres de 0 à 9, ainsi que d’un système de transmission de retenue. On peut les schématiser ainsi: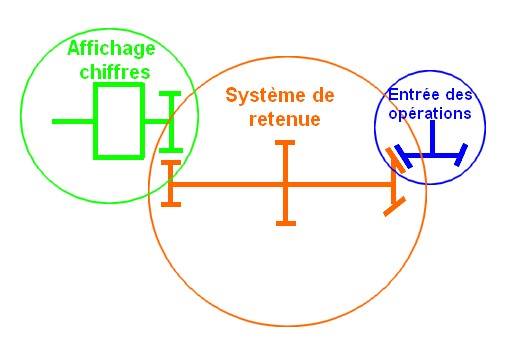

Ces derniers étaient ensuite disposés côte à côte afin de pouvoir afficher un nombre. On peut alors imaginer la Pascaline effectuer des opérations avec des nombres infiniment grands, pour peu qu’elle possède un nombre de ces blocs suffisant. Grâce à un système d’engrenages, l’utilisateur pouvait tourner les différentes roues d’entrée, afin d’afficher sur le rouleau le nombre de son choix. Les chiffres de 0 à 9 gravés sur les roues d’entrée autorisaient la saisie d’un nombre de façon rapide simple. La rotation du rouleau ne s’effectuait que dans le sens horaire, ainsi on pouvait faire défiler les chiffres de 0 vers 9 mais pas l’inverse. Ceci est primordial dans la réalisation d’opérations mathématiques via cette machine. Mais tout le génie de Blaise Pascal repose dans le système de transmission de la retenue. En effet, chaque bloc pouvait transmettre une retenue au bloc en amont. Ainsi lorsqu’un rouleau effectuait un tour complet, il provoquait la rotation d’un cran du rouleau en amont, traduisant ainsi le passage d’une retenue. Voici une vidéo (en anglais) permettant de mieux comprendre ce système.

Effectuer des additions était plutôt simple. Il suffisait à l’utilisateur d’entrer le premier nombre, puis d’entrer tous les nombres qu’il souhaitait lui additionner, un par un. Les retenues, alors transmises en cascade, permettaient à la machine d’afficher le résultat de l’addition de tous les nombres précédemment entrés dans la Pascaline. Ceci dit, il était nécessaire de « remettre la Pascaline à zéro» avant d’effectuer une nouvelle opération, afin de ne pas tronquer le résultat avec le nombre « mis en mémoire » dans l’appareil. Pour parvenir à cela, il suffisait de tourner chaque rouleau, en partant de celui le plus en aval puis en se décalant d’un étage à la fois, afin qu’il affiche 9. En tournant le rouleau le plus en aval d’un cran le chiffre 9999 se transforme alors en 0000 et la machine était « remise à zéro ». La réalisation de soustraction était légèrement plus complexe. Avant de se concentrer sur la démonstration mathématique, il est important de préciser que les rouleaux présentaient en réalité deux séries de chiffres : une série allant de 0 à 9 et une autre correspondant à leur complément à 9 (complément choisi en fonction de la base de la Pascaline ici en base 10) soit des chiffres allant de 9 à 0. Le complément à 9 d’un nombre N s’écrit ainsi:Les instructions de Pascal étaient alors les suivantes : pour faire une soustraction il suffisait de rentrer le complément à 9 du nombre auquel on souhaite soustraire quelque chose, puis le nombre que l’on souhaite soustraire à ce dernier. Le résultat de l’opération correspondait alors au nombre affiché dans la série des compléments à 9 de la machine. Ceci revient donc à effectuer cette opération: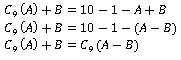Puis à regarder le complément à 9 du résultat de cette opération. Or on sait que:La Pascaline nous indique donc le nombre suivant, résultat correct de l’opération effectuée.Après nous être mis d’accord sur un design particulier, nous avons modélisé notre Pascaline sur ordinateur, via l’utilisation d’un logiciel tel que “Solidworks”. Voici le résultat : 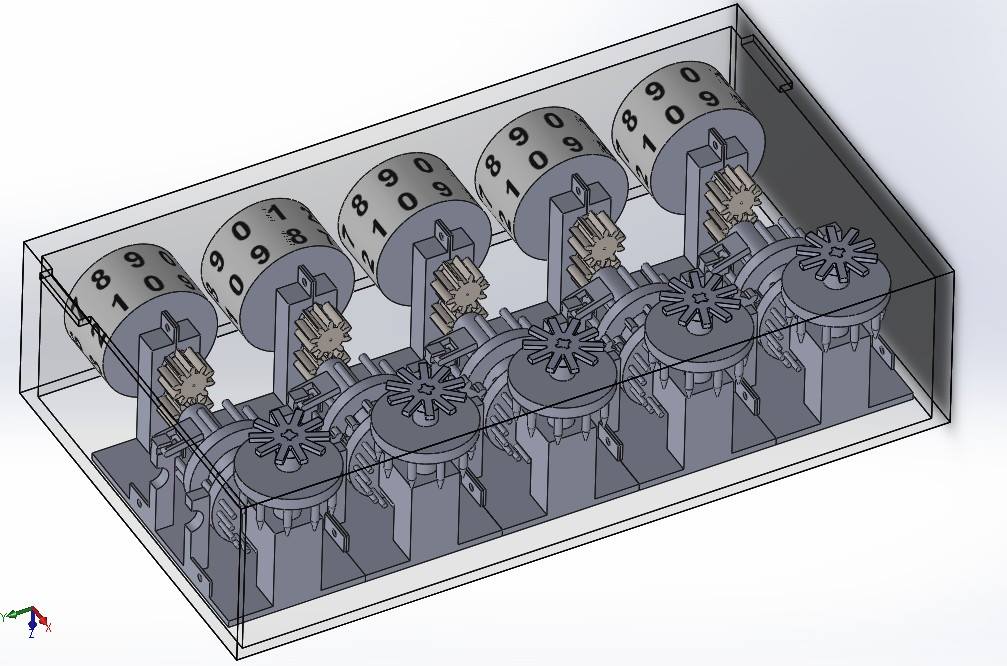Après 3 séances de dix-sept heures, et grâce à une imprimante 3D très précise, nous avons pu obtenir les multiples pièces précédemment conçues. Il nous a fallu ensuite, enlever l’excès de matière déposée par l’imprimante 3D puis contrôler la conformité des composants ainsi acquis.