Bonjour à tous,

Dans le cadre du dernier semestre de PEIP2, il nous est proposé de concevoir un projet par groupe d’étudiants. Nous sommes deux élèves à avoir travaillé sur ce projet, Paul Bolufer ainsi que moi-même Marc Berret. Le projet est encadré par des professeurs de l’école et a pour durée une centaine d’heures.

L’objectif de ce projet est de réaliser un simulateur permettant de modéliser le développement de certaines plantes. Pour notre part, nous avons choisi de le faire sous le langage Python. La modélisation s’appuie sur des modèles mathématiques.

1. Présentation du projet

La phyllotaxie est la science qui étudie l’ordre dans lequel sont implantées les feuilles, ou plus globalement la disposition des éléments d’un fruit, d’une fleur ou d’un bourgeon.

Nous avons ainsi décidé d’orienter notre projet vers la création d’un programme informatique permettant de simuler la disposition des feuilles lors de la croissance d’une plante.

Pour réaliser ce simulateur, il nous a été nécessaire d’acquérir de nouvelles compétences telles que:
– la maîtrise des outils mathématiques pour comprendre le comportement et l’évolution des plantes
– la maîtrise d’un outil informatique pour réaliser ces simulations

Et nous avons rapidement été confrontés à de premières contraintes comme:
– la nécessité de réaliser un travail de documentation sur le sujet
– comprendre les modèles mathématiques mis en jeu
– apprendre un nouveau langage de programmation (Python)

Il était alors important de bien structurer nos séances de travail, d’adopter une bonne organisation et de se partager les tâches afin de mener à bien notre projet.

2. Travail réalisé

Pour mener à bien ce projet, nous avons orienté notre travail en deux parties. Dans un premier temps, la documentation sur notre sujet, à savoir la phyllotaxie ainsi que les modèles mathématiques. Dans un seconde temps, la mise en pratique par le développement du simulateur sur le langage Python.

2.1 Documentation

Les différents types de phyllotaxie

Il suffit de changer l’angle pour obtenir une nouvelle forme de phyllotaxie. Il en existe 4 différentes:

Phyllotaxie verticillé :
Elle présente au moins trois organes par nœud. L’angle entre un nœud et le suivant est de 45 degrés. Ce cas de phyllotaxie est assez fréquent dans la nature.

Plants de véroniques de Virginie.

Phyllotaxie opposée :
Les feuilles sont opposées deux par deux et on observe une rotation de 90 degrés entre un nœud et le suivant.

Branches de menthe

Phyllotaxie spiralée :
Il s’agit de la forme la plus classique de phyllotaxie, on compte un seul organe par nœud et un angle de 137,5 degré entre un organe et le suivant. On la retrouve dans 92% des plantes.

Pomme de pin

Phyllotaxie alternée :
Elle présente une feuille par nœud et un angle de 180 degrés entre deux organes consécutifs.

Branche de chêne

Représentation mathématique en deux dimensions (théorie)

Pour dessiner les points, on utilise le repère polaire:
r = c * sqrt(n)
teta= n * angle
avec n est le nombre de points, c est la distance entre le point.

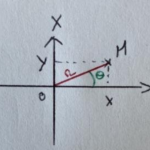
repère polaire

Nous pouvons passer du repère polaire au repère cartésien pour dessiner avec un code informatique. En effet, les langages de programmation ne comprennent pas le repère polaire.

Pour faire ceci, on utilise les propriétés du cosinus et du sinus qui sont respectivement:
cos = adj/hyp et sin = opp/hyp
On trouve que cos(teta)= x/r et sin()= y/r et ainsi x=cos(teta)*r et y=sin(teta)*r

Il suffira juste de faire une boucle en fonction de n et de préciser les paramètres de c et de l’angle.

2.2 Mise en pratique sur Python

Concrètement, une fois le sujet compris, il faut le retranscrire sur un programme informatique. Pour ce faire nous avons suivi des formations pour apprendre le langage Python.

Représentation de la phyllotaxie spiralée en deux dimensions (langage Python, éditeur VSC)

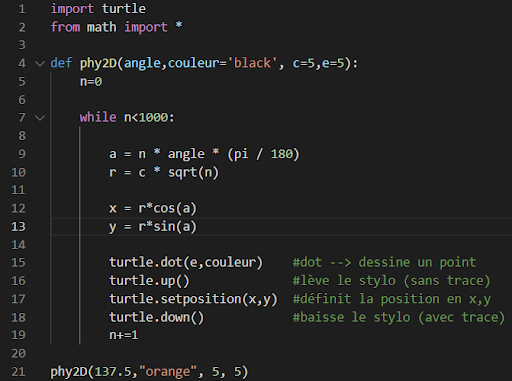
Code phyllotaxie en 2D sur Python

Explication du code:
Il faut tout d’abord importer les modules turtle et math nécessaire pour faire la représentation sous forme de dessins et pour utiliser les outils mathématiques. (ligne 1 et 2)

Ensuite, on crée la fonction phy2D (ligne 4) et on rentre les paramètres avec c la distance entre les points, e l’épaisseur. On fait une boucle qui va dessiner un grand nombre de points (n=1000).

On passe du repère polaire au cartésien. D’ailleurs, dans notre variable a (ligne 9), on convertit notre angle en radian en multipliant par pi/180 et par n pour que a dépend du point choisi. Puis, on dessine les points en changeant à chaque fois de position (x,y).

À la fin, il suffit simplement d’appeler la fonction en indiquant les paramètres et on obtient la figure ci-dessous:

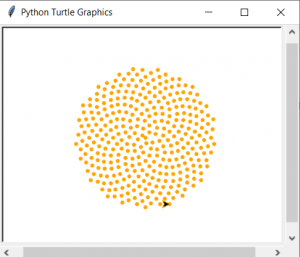
Représentation graphique de la phyllotaxie spiralée (angle d’or: 137.5 degrés)

Représentation en deux dimensions d’une marguerite et d’un tournesol

En s’appuyant sur le code précédent, on peut dessiner n’importe quelle plante en 2D. En effet, il suffit juste de créer des fonctions dessinant un pétale et les répéter le nombre de fois que l’on veut.

Simulation marguerite

Simulation tournesol

Création de l’application et d’un menu

Une fois que nos programmes pour représenter la phyllotaxie en 2D et avec des exemples concrets étaient fonctionnels sur Python, nous avons créé l’application pour les regrouper. Ainsi nous nous sommes aidés du module tkinter sur Python pour faire les boutons, le menu…

À gauche se trouvent les choix des différents paramètres et à droite l’interface graphique de dessin.

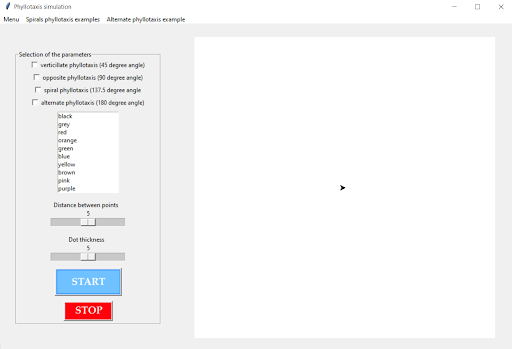
Interface principale du simulateur

Conclusion

Pour conclure, ce projet a été long mais motivant pour chacun d’entre nous. En effet, nous avons apprécié travailler en équipe. Nous sommes très fiers du travail réalisé et des notions que nous avons pu découvrir. Le résultat final est conforme au cahier des charges, tout au long de la réalisation de ce projet nous nous sommes adaptés à la fois aux modèles mathématiques ainsi qu’aux outils informatiques. Nous avons développé sous Python un simulateur complet permettant de modéliser la phyllotaxie en 2D mais aussi sous forme d’exemples avec le cas de la marguerite et du tournesol. Ce travail fut pour nous enrichissant, à la fois sur l’aspect des recherches, celui de la découverte mais aussi sur l’apprentissage d’un nouveau langage de programmation : Python.