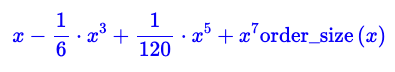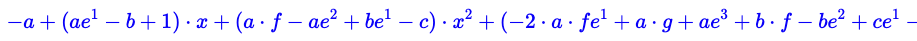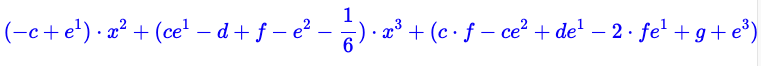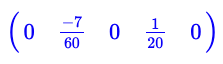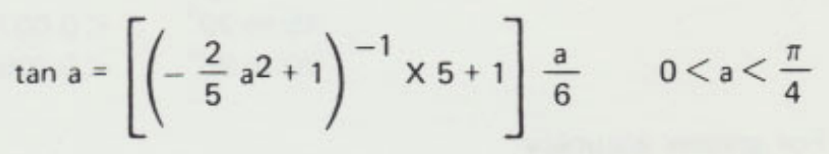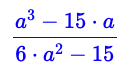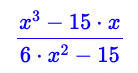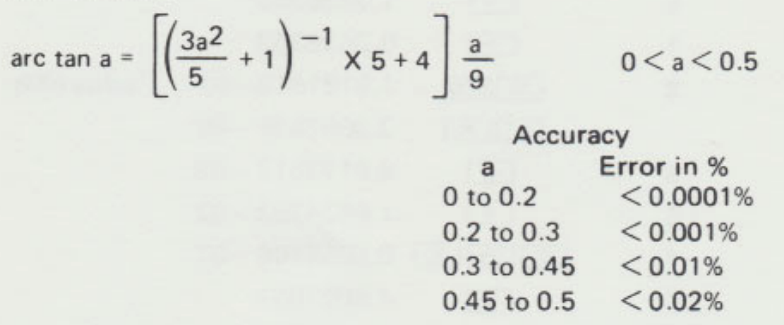Merci à la Gazette du site Silicium pour l’idée de cette recherche.

Page 27 du manuel de cette ancienne calculatrice (Texas Instrument SR-16 de 1975), on peut voir cette formule :

Elle ne ressemble pas au développement classique de Taylor où l’on a un polynôme suivi d’un reste :

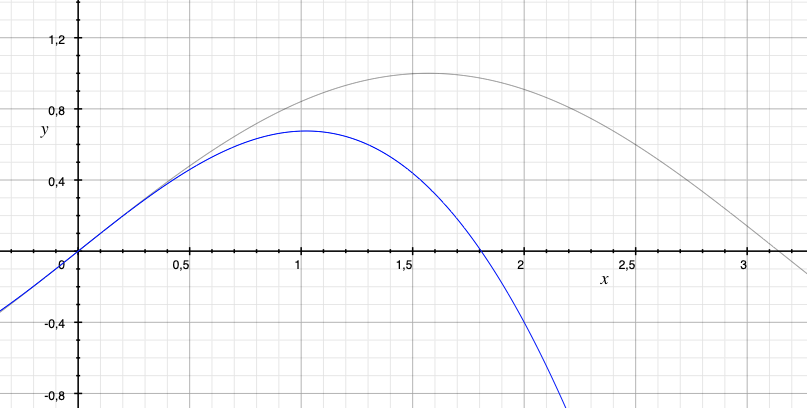
D’ailleurs cette approximation est vite mauvaise comme on peut le voir sur ce graphique :

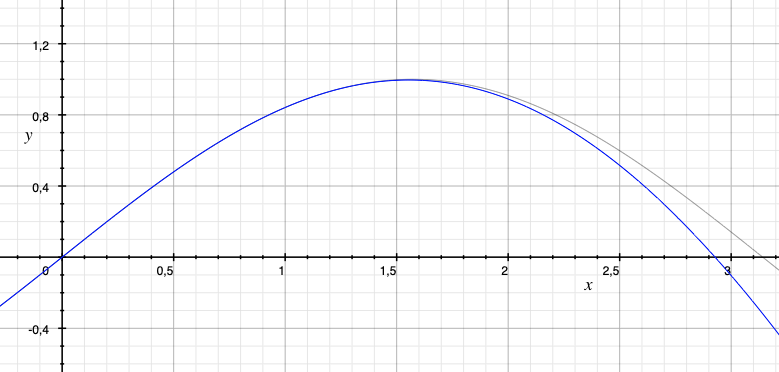
Or si on trace la fonction proposée dans le manuel, on obtient :

La technique mathématique utilisée est celle des approximants de Padé. Voici comment avec XCas, logiciel de calcul formel, on peut retrouver la formule :

On décide de chercher une approximation de sin(x) sous la forme d’une fraction rationnelle (polynôme divisé par un polynôme). On se fixe les degrés de ces polynômes au numérateur et au dénominateur, par exemple 3 pour les deux.

On fait le développement de Taylor de la différence entre la fonction sinus et notre fraction :

taylor(sin(x)-(a+b*x+c*x^2+d*x^3)/(1+e*x+f*x^2+g*x^3),x=0,6)

On trouve les premiers termes :

L’idée est d’annuler les différents coefficients pour que la différence soit la plus petite possible, on trouve tout de suite a = 0 et b = 1. Développons la nouvelle expression et convertissons le résultat en polynôme :

P:=convert(taylor(sin(x)-(x+c*x^2+d*x^3)/(1+e*x+f*x^2+g*x^3),x=0,6), polynom)

Résolvons le système d’équations (non linéaire) à 5 inconnues :

solve(coeffs(P),[c,d,e,f,g])

La fraction rationnelle cherchée s’écrit donc :

F:=(x-7/60*x^3)/(1+1/20*x^2)

Ou encore, en simplifiant :

C’est exactement la formule proposée dans le manuel puisque :

simplify((10/(x*x/20+1)-7)*x/3)

donne la même chose !

Remarque : Le logiciel Xcas a la fonction pade et permet de retrouver le résultat immédiatement. Ci-dessous le « 4 » pour avoir des polynômes de degrés < 4 et le « 5 » pour avoir un développement jusqu’à l’ordre 5 :

pade(sin(x),x,5,4)

(-7*x**3+60*x)/(3*x**2+60)

Formule pour la tangente

simplify((5/(1-2*a^2/5)+1)*a/6)

P:=convert(taylor(tan(x)-(a+b*x+c*x^2+d*x^3)/(1+e*x+f*x^2+g*x^3),x=0,6),polynom)

donne :

-a+(a*e-b+1)*x+(a*f-a*e)**2+b*e-c)*x**2+...

D'où a = 0 et b = 1

P:=convert(taylor(tan(x)-(x+c*x^2+d*x^3)/(1+e*x+f*x^2+g*x^3),x=0,6),polynom)
solve(coeffs(P),[c,d,e,f,g])

ce qui permet d'obtenir :

[0,-1/15,0,-2/5,0]

d'où la fraction :

F:=simplify((x-1/15*x^3)/(1-2/5*x^2))

pade(tan(x),x,5,4)

(x**3-15*x)/(6*x**2-15)

A propos de leur formule pour atan

En utilisant la fonction pade de XCas, avec des polynômes de degrés 3 au maximum on obtient :

pade(atan(x),x,4,5)

La formule parait nettement plus simple ! Traçons les 3 courbes sur un même graphique (atan, celle du manuel et celle d’XCas) :

Les courbes semblent être plutôt proches de atan pour 0 < x < 0.5. Cherchons l’erreur relative dans les 2 cas quand x = 0.5 :

Formule du manuel :

ma(x):=(5/(3*x^2/5+1)+4)*x/9

Formule proposée par XCas :

xc(x):=(-x**3+3*x)/3

Valeur attendue :

a:=atan(.5)

Erreurs relatives dans les 2 cas en % :

100*abs(ma(.5)-a)/a

donne 0.025991 soit environ 0.02 % comme décrit dans le manuel

100*abs(xc(.5)-a)/a

donne 1.14618 soit environ 1.14 %

La formule proposée par le manuel est donc bien meilleure pour la valeur extrême.