Vous pouvez tester par copier/coller les différents codes ici : https://console.basthon.fr/

Cette page reprend la traduction en Processing Python de script trouvés sur la page Twitter d’Akira.

Si vous ne connaissez pas P5 version Python, voici mes vidéos d’initiation :

Animations complexes

Roue colorée (d’après un tweet d’Akira twitter.com/akira2768922)

Code à copier/coller dans https://console.basthon.fr/ puis Exécuter

from p5 import *
from math import pi

def A(a):
  for n in range(9):
    stroke(0 if a else 7)
    T(0, 45)
    fill((8 - n + int(f)) % 8, 2, 8)
    box(2, 89)
    T(0, 45)
    Z(a)

def setup():
    global T, Z, P, f
    createCanvas(900, 600, WEBGL)
    colorMode(HSB, 8)
    T, Z = translate, rotateZ
    P, f = pi / 4, 0

def draw():
    global f
    background(7)
    rotateX(12)
    Z(2 * P)
    T(90, f % 1 * 90 - 90)
    push()
    A(0)  
    pop()
    Z(f % 1 * P)
    A(P)
    f += .05
  
run() 

Chainette (d’après Akira)

from p5 import *
from math import pi

def setup():
    global T, Y, P, f, W
    W = 600
    createCanvas(W, W, WEBGL)
    T, Y = translate, rotateY
    f = 0
    noStroke()
    frameRate(40)

def draw():
    global f
    background(0)
    f += 1
    T(0, -W, 300)
    Y(pi / 60 * f)
    for i in [5, 9, -9]:
      j = -i * W    
      spotLight(W, W, W, j, j, 0, i, i, 0)
    for j in range(30,0,-1):
        T(8,34)
        for i in range(200,0,-1):
            T(0,.5)
            sphere(3)
            if int(i / 50) % 2: rotateZ(pi / 50)
        T(-8, 0)
        Y(pi / 2)

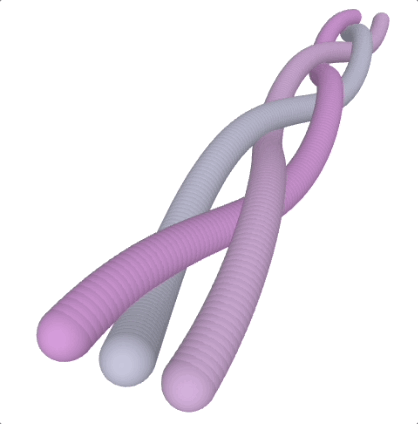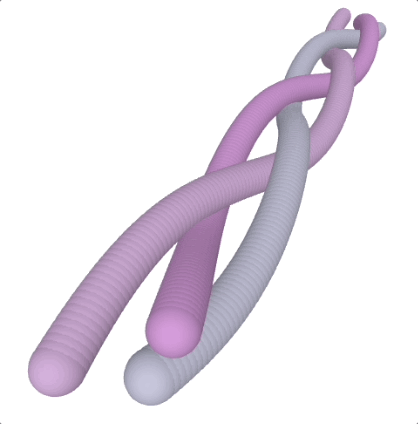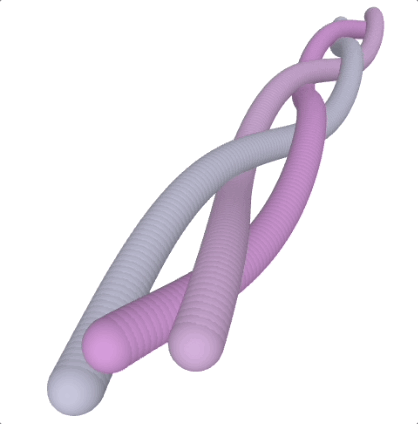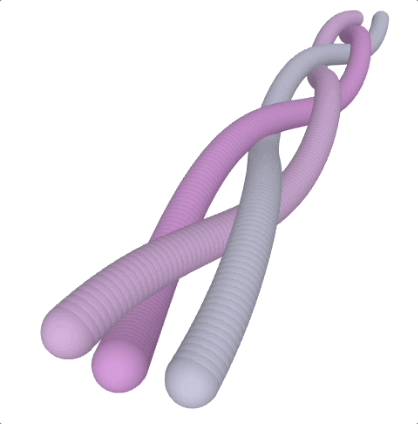
run() 

Scoubidou

from p5 import *
from math import pi, sin

def setup():
    global t, W
    W = 600
    createCanvas(W, W, WEBGL)
    t = 0

def draw():
    global t
    background(W)
    noStroke()
    lights()    
    t += 1
    for j in range(3, 0, -1):
      for i in range(W // 3):
          push()
          fill(210 + j * 20, 250 - j * 20, 255)
          r = pi * (i - t + j * 120) / 90
          translate(50 * sin(r) - 70 + i * 2, \
                    20 * sin(r * 2) - i * 3 + 90, \
                    200 - i * 4)
          sphere(20)
          pop()

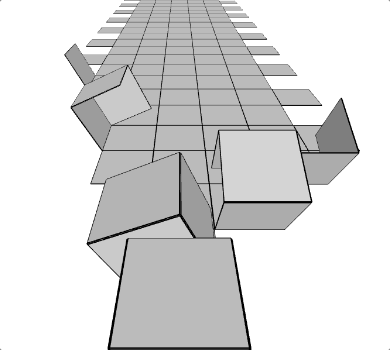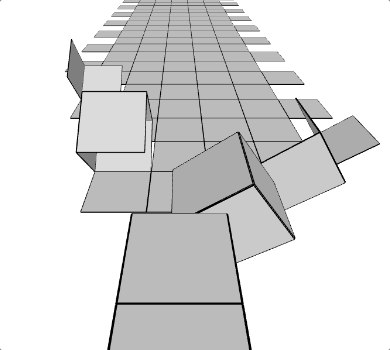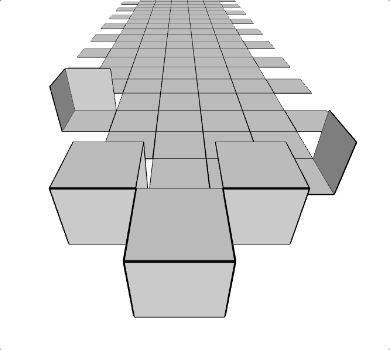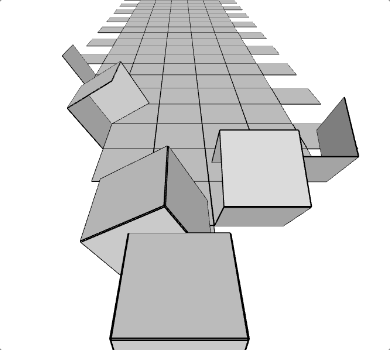
run() 

Développement d’un cube (script Akira)

from p5 import *
from math import pi, cos

def setup():
    global t, T
    createCanvas(900, 600, WEBGL)
    colorMode(HSB, 6)
    T = translate
    t = 0

def draw():
    global t
    t += .01
    u = cos(t)
    r = (u + 1) * pi / 4
    background(200)
    p = -150 + 50 * u 
    T(p, p, -50)
    for i in range(6):
        fill(i, 4, 6, 3)
        square(0, 0, 100)
        if i % 2:
            T(0, 100, 0)
            rotateX(r)
        else:
            T(100, 0, 0)
            rotateY(-r)
    
run() 

Marches (script Akira)

from p5 import *

def setup():
    global t, Y
    createCanvas(900, 600, WEBGL)
    Y = rotateY
    t = 0
    colorMode(HSB,9)

def draw():
    global t
    background(240)
    t += .01
    rotateX(-.2)
    Y(.3)
    for i in range(31):
        push()
        u = t % 1       
        Y((-21 + i + u) / 3)
        translate(0,(22 - i - u) * 40, 180)
        if i < 21:
            fill(7,4)
            stroke(3)
        else:
            c = (t - u + 30 - i) % 9
            fill(c, 5, 9, 4)
            stroke(c, 5, 9)
        box(60, 9, 120)
        pop()  
    translate(0, (u - .5) ** 2 * 180 - 20, 180)
    rotateZ(-TAU * u)
    fill(t % 9, 5, 9, 5)
    stroke(t % 9, 5, 8)    
    box(20)       
run()

Pendule de newton (script akira)

from p5 import *
from math import pi, cos

def setup():
    global f, W, T
    W = 600
    createCanvas(900, W, WEBGL)
    f, T = 0, translate

def draw():
    global f
    background(0)
    noStroke()
    f += 1
    for i in [5, 9, -9]:
      j = -i * W    
      spotLight(W, W, W, j, j, 0, i, i, 0)
    for n in range(24,0,-1):
        push()
        T(0, -300, 30 * n - W)
        rotateZ(cos(pi * f / 1800 * (60 - n)) / 2)
        l = 120 + 5 * n 
        T(0, l)
        cylinder(1, 2 * l)
        T(0, l)
        ellipsoid(20)
        pop()
run() 

Cercles concentriques

from p5 import *

def setup():
    global f,W
    W = 600
    createCanvas(900, W, WEBGL)
    f = 0

def draw():
    global f
    background(0)
    noStroke()
    f += 1
    for i in [5, 8, -9]:
      j = -i * W    
      spotLight(W, W, W, j, j, 0, i, i, 0)
    for n in range(9,0,-1):
        r = 30 * n + 1
        torus(r, 9, 99)
        for a in [-1,1]:
            push()
            translate(0, (r + 15) * a)
            cylinder(3, 9)
            pop()
        rotateZ(.4)
        rotateY(TAU * f / W)
run() 

Rangements de cartons

from p5 import *
from math import pi

def setup():
    global t, W, T, X, Z
    W = 600
    createCanvas(900, W, WEBGL)
    t, T, X, Z = 0, translate, rotateX, rotateZ

def draw():
    global t
    background(W)
    lights()
    t += 1
    Q = pi / 2
    rotateY(Q)
    Z(.9)
    for j in range(26, 0, -1):
        push()
        u = t / 60 % 2
        T(0, 98 * (u - j + 3))
        X(0 if j % 2 else 2*Q)
        for i in range(6, 0, -1):
            box(1, 97)
            X(-Q if i % 2 else Q)
            T(0, 49)
            Z(map(i - u + j, 7, 8, Q, 0, 1))
            T(0, 49)
        pop()	
run() 

Boules

Le code ci-dessous est une adaptation en Python d’un script de Koma Tebe

from p5 import *

def setup():
    global f, W, T
    W, T = 400, translate
    createCanvas(900, W, WEBGL)
    f = 0

def draw():
	global f
	background(0)
	f += 1
	rotateX(-.8)
	for i in [W, -W, 100]: pointLight([i],0,-i,i)
	i = 0
	while i < TAU:
		i += TAU / 5000
		push()
		rotateY(noise(i * W) * TAU * 2)
		F = (f + 100 * i) % W + i
		Y = -100 * abs(sin(f / 44 - F / 33))
		T(F, Y)
		fill(-3 * Y)
		sphere(4 - F / 100, W)
		pop()		

run() 

Escargot (script de Koma Tebe)

from p5 import *
from math import sin, cos

def setup():
    global f, W, T
    W, T = 400, translate
    createCanvas(600, W, WEBGL)
    f = 0
    frameRate(20)

def draw():
    global f
    background(0)
    for i in [8,-8,9]: spotLight(W,W,W,0,-W*i,W,0,i,-1)
    for j in range(64):
        i = PI * j / 64
        push()
        rotate(i * sin(i + f / 9))
        T(6 * i, i)
        rotateX(2 * i * cos(i - f / 9))
        torus(40 * i, 2 * TAU - 2 * i, W)
        scale(noise(i - f) / .8)
        pop()
        f += .01
	
run()