J’ai une passion pour les calculatrices et les langages minimalistes (écrire peu, faire beaucoup). C’est le cas du langage RPL sur les calculateurs HP, du langage APL, des machines n’ayant que quelques octets (Ti 57 = 50 pas de programme), etc.
Suite à mes prospections autour du langage K, que je trouve infiniment plus attractif que le langage J d’Iverson, j’ai découvert oK (correspondant à la version K6, le langage K ayant des numéros avec plusieurs spécifications) et qui existe en version mobile :


La version proposée sur le site officiel nécessite d’avoir un téléphone (ou une tablette) connecté à Internet (à cause de 2 fichiers : base-min.css et Chart.min.js), ce qui est dommage. C’est pourquoi vous trouverez ici une version avec ces 2 fichiers déjà téléchargés. L’ensemble ne fait que 200 ko dont 144 ko juste pour Chart.min.js dont on peut se passer si on ne veut pas de graphique !
Petit survol de oK Mobile
Si vous testez oK Mobile sur ordinateur, il faudra diminuer la largeur de la fenêtre jusqu’à obtenir l’interface en mode Portrait (comme sur un téléphone). Vous pourrez bien entendu utiliser les touches de votre clavier. Vous pouvez aussi rester en mode paysage mais utilisez la touche MAJ (SHIFT) pour voir des caractères supplémentaires.
/ On a les réductions :
+/ !10 / !10 correspond à 0 1 2 ... 10
45
/ ":" pour imposer l'utilisation monadique de #
/ Nb de caractères de chaque mot
#:'("bonjour";"tout";"le";"monde")
7 4 2 5
|/ 3 5 4 2 / Maximum
5
&/ 3 5 4 2 / Minimum
2
/ Convergence vers le nombre d'or
{1+1%x}/1
1.618
/ Aucun changement pour l'exercice "gimme" que j'avais proposé
*1_< 8 5 12 / Tri + suppr 1er élément + Récup 1er
0
/ But : Ne pas garder les notes inférieures à 10
{x<10}_ 5 6 10 18 1 17
10 18 17
/ Reste de la division de 27 par 5
5!27
2
/ But : Garder les multiples de 5
/ la négation ~ permet d'avoir des 1...
/ ...lorsque x est divisible par 5 et 0 sinon
{~5!x}# 3 15 21 20 17
15 20
/ autre version
/ on enlève les "non multiple de 5"
(5!)_ 3 15 21 20 17
15 20
/ Fonction carrée
c:{x*x}
c 8 9
64 81
/ Fonction de 2 variables
/ 13 = 1 + 3 * 4 ; 17 = 2 + 3 * 5 et 21 = 3 + 3 * 6
f:{x+3*y}
f[1 2 3; 4 5 6]
13 17 21
/ Combien y-a-t-il d'éléments dans t et quelle est la valeur max ?
t: 5 3 8 1 2
{(#x),|/x} t
5 8 / 5 éléments et max = 8
/ Répartition des indices suivant les valeurs
= "abracadabra"
"abrcd"!(0 3 5 7 10
1 8
2 9
,4
,6)
En route pour Syracuse
Dans la plupart des vidéos consacrées aux calculatrices, je propose la conjecture de Syracuse, à savoir partir d’un nombre entier, s’il est pair le diviser par 2 sinon le multiplier par 3 et ajouter 1. La conjecture prétend que l’on arrivera toujours à un moment à la valeur 1.
Commençons par une version simple :
syr:{$[2!x;1+3*x;x%2]}
/ 2!27 vaut 1 (reste division de 27 par 2) qui correspond à VRAI
/ donc le nombre est multiplié par 3 plus 1
syr 27
82
/ 2!82 vaut 0 qui correspond à FAUX
/ donc le nombre est divisé par 2
syr 82
41Où $ correspond au test SI ALORS SINON : $[test ; valeur_si_Vrai ; valeur_si_Faux]
Cumulons les conditions, par exemple, si x<2 renvoyer 1 sinon, si impair alors… etc.
syr:{$[x<2;1;2!x;1+3*x;x%2]}
syr 27
82
syr 1
1 / et non pas 4On peut alors faire un scan-fixedpoint \ (scanner tant que l’on n’a pas obtenu une valeur fixe). La valeur fixe est ici 1.
syr:{$[2>x;1;2!x;1+3*x;x%2]}\
syr 5
5 16 8 4 2 1Mais on peut écrire cela de façon encore plus conviviale avec scan-while (scanner tant que). L’écriture ci-dessous signifie : répéter {$…} tant que x>1
syr:{x>1}{$[2!x;1+3*x;x%2]}\
syr 5
5 16 8 4 2 1On peut alors chercher le temps de vol et le maximum :
stats:{(#1_x),|/x}
stats syr 5
5 16 / temps de vol = 5 et max = 16
stats syr 27
111 9232On peut même faire un graphique :
r:syr 27
pl[#r;r] / Plot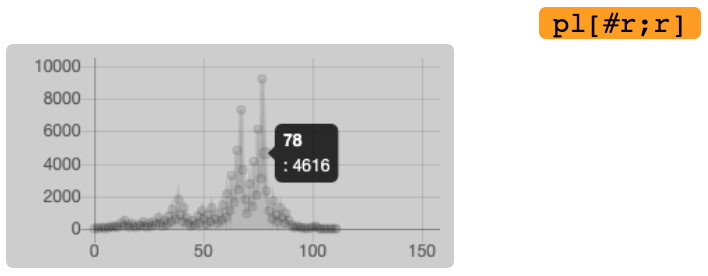
Autres exemples tirés de mes vidéos sur l’APL ou du forum Silicium
Vous trouverez mes 3 vidéos sur APL ici et les MPO APL sur Silicium.
Sushis (vidéo n°1 sur APL)
2 EUR le sushis (représentés par « s »), combien va-t-on payer si on en a mangé » s sss ss » ?
sushis:2*+/"s"=
sushis " s sss ss"
12Brin d’ADN (vidéo n°1 sur APL)
Est-ce qu’une chaine est un brin d’ADN, c’est-à-dire qu’elle ne contient que les lettres A, C, T et G.
adn:~|/^"actg"?_ / Version n°1
adn "acccxtg"
0
adn "atttCgTgtA"
1
/ Explications :
"actg"?_ "tgcaxa"
2 3 1 0 0N 0 / 0N signifie Not a Number (NaN)
^ 2 3 1 0 0N 0 / ^ teste si l'élément est NaN
0 0 0 0 1 0
/ On prend la plus grande valeur et négation
/ donc s'il y a un "1" ce n'est pas un brin d'ADN
adn:{&/(_x) in "actg"} / Version n°2
/ La réduction &/ correspond à la recherche du minimum
/ "x in y" renvoie Vrai ou Faux suivant que x est dans y ou non
"a" in "actg"
1 / "a" est bien dans "actg"
"abc" in "actg"
1 0 1 / "a" et "c" sont dans "actg", pas "b"Récupérer les lettres qui sont différentes de A,C,T,G :
adn:{(_x) in "actg"}_ / Version 1
adn "auccfCCWG"
"ufW"
adn:{(_x)^"actg"} / Version 2Nettoyage des chiffres (vidéo n°1 sur APL)
Enlever les chiffres qui sont dans une chaine « s4402a25l8u9t005 » -> « salut »
net:{x in ,/$:'!10}_
net "s4402a25l8u9t005"
"salut"
/ !10 pour avoir la liste 0 1 2 ... 9
/ $:' pour transformer chaque chiffre en chaine
/ ,/ pour concaténer ces chaines -> "0123456789"
/ pour finir on enlève (_) ceux qui ne sont pas dans cette chaineAutant de « X » que de « o » ? (vidéo n°1 sur APL)
Y a-t-il autant de « x » que de « o » dans une chaine donnée ?
xo:{0=+/(x="x")-x="o"
xo "xoox"
1
xo "xoxoo"
0RATP (vidéo n°2 sur APL)
Récupérer les initiales des mots d’une phrase :
s:*:'" "\
s "rentre avec tes pieds"
"ratp"
/ Ou encore, si on entre les mots dans une liste
s:*:'
s ("rentre";"avec";"tes";"pieds")
"ratp"Meilleur score de chaque équipe (vidéo n°2 sur APL)
Récupérer le meilleur score de chacune de ses trois équipes :
/ Equipe n°1 : 4, 8 et 9
/ Equipe n°2 : 5, 10 et 3
/ Equipe n°3 : 7 et 12
scores:((4;8;9);(5;10;3);(7;12))
best:|/'
best scores
9 10 12Lettre la plus éloignée dans l’alphabet (vidéo n°2 sur APL)
Dans une chaine, trouver la lettre la plus éloignée dans l’alphabet
max:{*x[>x]}
txt:"LA MODE SE DEMODE, LE STYLE JAMAIS"
max txt
"Y"Misez p’tit, Optimisez – N°10 (hommage à J. McCarthy)
Enoncé : Misez p’tit, Optimisez – N°10 (hommage à J. McCarthy)
MPO10:{$[x>100;x-10;o(o(x+11))]}
MPO10 5
91
MPO10 0
91
/ "o" permet de faire un appel récursifMisez p’tit, Optimisez – N°15 (le jour des fourmis)
Enoncé : Misez p’tit, Optimisez – N°15 (le jour des fourmis)
MPO15:{,/(#:'.s),'!s:=x@>x}\,
MPO15 0
(,0
1 0
1 1 1 0
3 1 1 0
1 3 2 1 1 0
1 3 1 2 3 1 1 0
2 3 1 2 4 1 1 0
1 4 1 3 2 2 3 1 1 0
1 4 2 3 2 2 4 1 1 0
2 4 1 3 3 2 3 1 1 0
1 4 3 3 2 2 3 1 1 0)Quelques explications :
– x@>x permet de trier les valeurs de la liste, par exemple 1 0 3 1 devient 3 1 1 0
– Le = fait les statistiques (compte le nombre d’occurrences de chaque valeur)
– On mémorise dans s le résultat qui se trouve être un dictionnaire donnant les positions, par exemple 1 0 3 1 donnera 3 1 0!(,0 ; 1 2 ; ,3). En effet, une fois trié, 1 0 3 1 donne 3 1 1 0, le « 3 » est à la position 0, le « 1 » aux positions 1 et 2 et le « 0 » à la position 3
– Les caractères ! et . permettent de récupérer les clés et les valeurs d’un dictionnaire
– La virgule pour la concaténation, l’apostrophe pour dire « pour chaque » et le # pour compter
– Le symbole \ à droite permet de boucler la fonction entre accolades tant que le résultat n’est pas stable.
En français, on pourrait donc dire : Tant que le résultat n’est pas stable, trier les éléments par ordre croissant, compter les occurrences des chiffres distincts puis concaténer l’effectif avec la valeur.
Pas à pas sur un exemple :
MPO15 1 0 3 1
{x@>x} 1 0 3 1 / Tri
3 1 1 0
{=x@<x} 1 0 3 1 / Stats
3 1 0!(,0 / une seule position pour "trois"
1 2 / deux positions pour "un"
,3) / une position pour "zéro"
{!s:=x@>x} 1 0 3 1 / On mémorise dans s et récupération clés
3 1 0 / Ceux sont les valeurs distinctes
{#:'.s:=x@<x} 1 0 3 1 / On compte le nombre de valeurs
1 2 1
1 2 1 ,' 3 1 0 / Concaténation élément par élément
(1 3 / il y a un "trois"
2 1 / il y a deux "un"
1 0) / il y a un "zéro"
,/ 1 2 1 ,' 3 1 0 / Concaténation de l'ensemble
1 3 2 1 1 0 Misez p’tit Optimisez n°96 : Combien de bits à un dans cet entier ?
Enoncé : Misez p’tit Optimisez n°96 : Combien de bits à un dans cet entier ?
MPO96:{$[1>x;0;(2!x)+o(_x%2)]}
MPO96 1279
9J’ai repris l’idée de @C.Ret d’utiliser un algorithme récursif. Tant que le nombre x est plus grand que 0, on cherche son reste en le divisant par 2 (donc 1 s’il est impair) et on a ajoute la valeur obtenue par le même algorithme à la moitié de x (_x%2 : partie entière de x divisé par 2)
L’inconvénient est que l’on dépasse assez vite le nombre d’appels à la pile :
MPO96 31415926
Maximum call stack size exceededOn peut aussi répondre à la question en utilisant decode (\). Le problème est qu’il faut connaitre le nombre de bits à afficher :
2 2 2 2 \ 7
0 1 1 1 / Affichage de 7 sur 4 bits
2 2 2 2 \ 16
0 0 0 0 / 16 sur 4 bits donne 0 !
2 2 2 2 2 \ 16
1 0 0 0 0 / et résultat correct sur 5 bitsLe nombre de bits à utiliser est 1 + ln(x) / ln(2). Comme 1 / ln(2) vaut environ 1,44, on a cette autre version :
MPO96:{+/((1+1.5*log x)#2)\x}
MPO96 31415926
18
MPO96 314159265358979323846
30
/ Pour dupliquer une valeur on utilise #
6 # 2
2 2 2 2 2 2
3.14 # 2
2 2 2 2Produits intérieur et extérieur
produit intérieur
L’exemple le plus commun est la somme des produits (SOMMEPROD avec Excel) :
+/*[4 2 3;1 5 6] / 4*1 + 2*5 + 3*6 = 32
32
/ que l'on pourrait également écrire :
{+/x*y}[4 2 3;1 5 6]
32
/ Le plus petit des plus grands entre (4,1), (2,5), (3,6)
&/|[4 2 3;1 5 6]
4
/ En effet, les plus grands 2 à 2 sont : 4 5 6
/ et le plus petit des 3 est 4
/ Tous les nombres sont-ils plus petits que 10 ?
/ Il fait les comparaisons 4<10, 5<10 et 6<10 (soit 1 1 1)
/ puis cherche le minimum des résultats (ici 1)
&/<[4 5 6;10]
1
&/<[4 5 16;10]
0produit extérieur
Commençons par la classique table de multiplication :
*\:[n;n:1+!5]
(1 2 3 4 5
2 4 6 8 10
3 6 9 12 15
4 8 12 16 20
5 10 15 20 25)
/ Explications :
1+!5
1 2 3 4 5
/ que l'on mémorise dans "n"
/ On effectue les produits de tous les éléments de n...
/ ... par tous les éléments de n soit n*n résultats
=\:["xo";"xxooxo"]
(1 1 0 0 1 0
0 0 1 1 0 1)
/ Explications :
/ On compare un par un les éléments de "xo" avec ceux de "xxooxo"L’exemple classique en APL de la création d’un histogramme :
v:2 7 1 8 2
".0"[>\:[v;!|/v]]
("00......"
"0000000."
"0......."
"00000000"
"00......")
/ Explications :
/ On cherche la plus grande valeur de v
|/v
8
/ ce qui permet de créer la liste
!|/v
0 1 2 3 4 5 6 7
/ Ensuite, on compare (>) chaque valeur de v avec cette liste
>\:[v;!|/v]
(1 1 0 0 0 0 0 0
1 1 1 1 1 1 1 0
1 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1
1 1 0 0 0 0 0 0)
/ et finalement on remplace les 0 par des "." et les 1 par des "0"combien sont plus grands que moi (vidéo n°3 sur APL)
A partir d’une liste de nombres, dire pour chacun combien sont plus grands qu’eux. Par exemple avec 1 30 4 16 5 1 8, il y a 5 nombres plus grands que 1, 0 plus grands que 30, 4 plus grands que 4 etc. On doit donc obtenir 5 0 4 1 3 5 2.
v:1 30 4 16 5 1 8
1 30 4 16 5 1 8
taille:{+/'<\:[x;x]}
taille v
5 0 4 1 3 5 2
/ Explications
/ On compare chaque élément de v avec chaque élément de v
<\:[v;v]
(0 1 1 1 1 0 1
0 0 0 0 0 0 0
0 1 0 1 1 0 1
0 1 0 0 0 0 0
0 1 0 1 0 0 1
0 1 1 1 1 0 1
0 1 0 1 0 0 0)
/ Et on fait la réduction par la somme (+/) pour chaque (') ligneAnnées bissextiles (vidéo n°3 sur APL)
Les explications de la formule sont dans la vidéo.
annees:1900 2020 2024 1901 2023 / Années à tester
biss:(=/~400 100 4 !\:)#
biss annees
2020 2024
/ Explications
/ Calcul des restes des divisions par 400, 100 et 4
400 100 4 !\:annees
(300 20 24 301 23
0 20 24 1 23
0 0 0 1 3)
/ On cherche où sont les "0"
~400 100 4 !\:annees
(0 0 0 0 0
1 0 0 0 0
1 1 1 0 0)
/ Réduction par colonne en testant si égalité (=/)
=/~400 100 4 !\:annees
0 1 1 0 0
/ et finalement on garde (#) les années où il y a "1"Tableau résumé
| +/.:’$ N | Somme des chiffres de l’entier N |
| {1+1%x}/1 | Convergence vers le nombre d’or |
| {x<N}_ V | Supprime du vecteur V les éléments < à N |
| (N!)_ V | Garde du vecteur V uniquement les multiples de N |
| ~|/^ »actg »?_ S | Teste si la chaine S est un brin d’ADN |
| *:' » « \ S | Initiales des mots séparés par espace dans une chaine S |
| {*x[>x]} S | Lettre la plus éloignée dans l’alphabet d’une chaine S |
| &/<[V;N] | Tous les éléments de V sont-ils < à N ? |
| *\:[n;n:1+!N] | Table de multiplication des entiers de 1 à N par eux-mêmes |
| =\:[S1;S2] | Comparaisons de toutes les lettres de S1 avec celles de S2 |
| {+/'<\:[x;x]} V | Pour chaque élément de V, compte combien sont plus grands |
| (=/~400 100 4 !\:)# V | Filtre les années bissextiles qui sont dans V |
