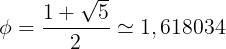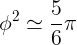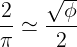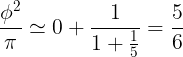Exercices autour des pyramides

A télécharger : Enoncé et corrigé au format Word

Exercice 1 – Pyramide et nombre d’or

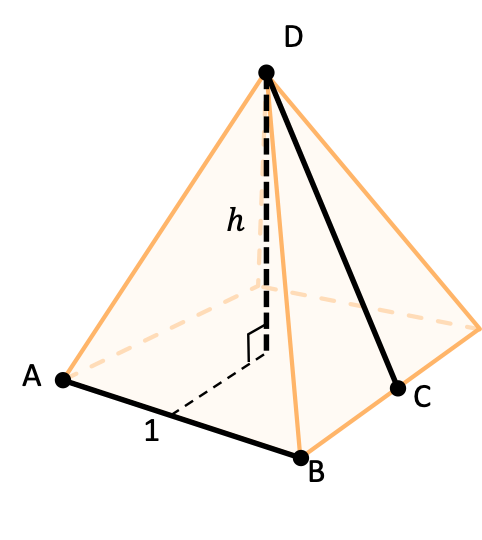
Ci-dessous un carré de côté AB = 1. On ajoute 4 triangles isocèles de hauteur CD.

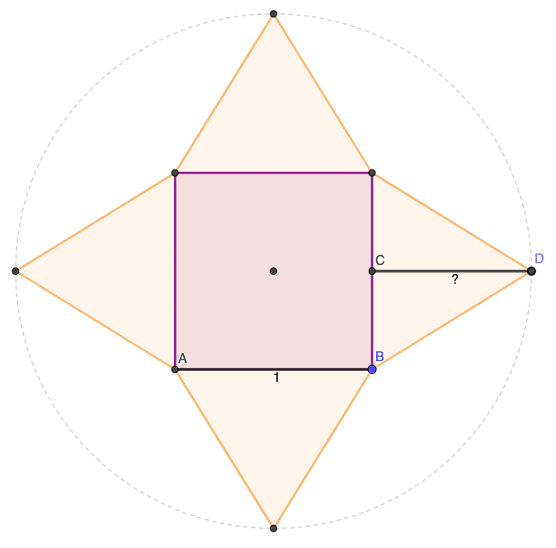
Q1. Trouvez la longueur CD telle que l’aire totale des 4 triangles soit égale au nombre d’or 𝜙

Le nombre d’or vaut :

Q2. En déduire la hauteur ℎ de la pyramide que l’on obtient :

Application numérique :

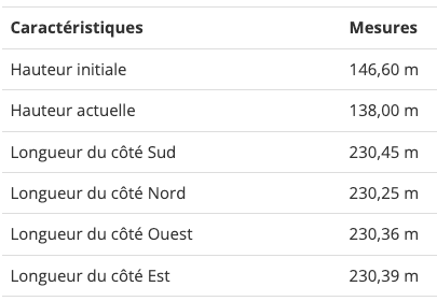
Voici les caractéristiques de la pyramide de Khéops (sur le plateau de Gizeh, en Égypte) :

Q3. Calculez la longueur moyenne m des 4 côtés de la base de la pyramide de Khéops.

On suppose maintenant que AB est égale à la longueur moyenne m trouvée à la question 3.

Q4. Quelle hauteur h doit avoir la pyramide pour que le quotient de l’aire visible (les 4 triangles) par l’aire invisible (la base carrée) soit égale au nombre d’or ?

Q5. Calculez en pourcentage l’erreur relative entre la hauteur h trouvée à la question 4 et la hauteur réelle 146,60 m

On appelle erreur relative la quantité : (valeur_approchée – valeur_réelle) / valeur_réelle

Exercice 2 – Coudée royale

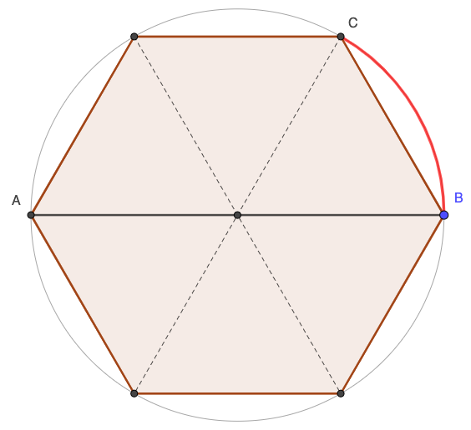
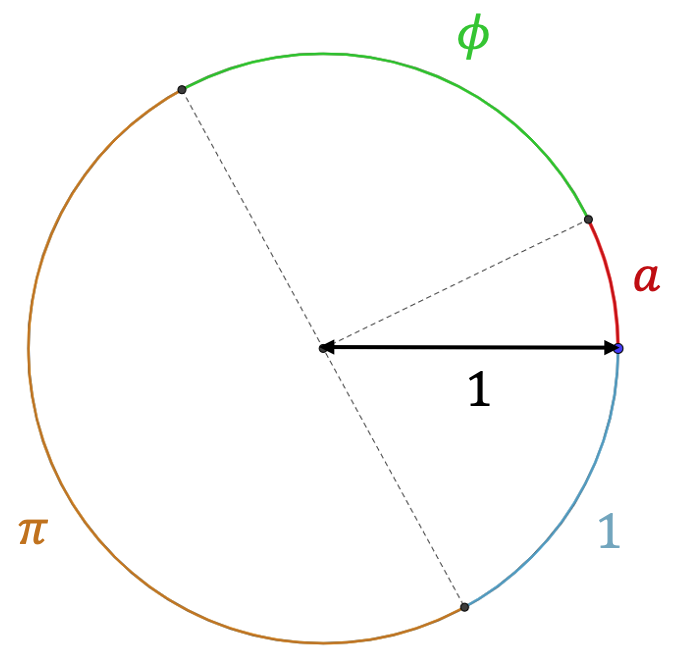
On suppose que le diamètre du cercle sur la figure ci-dessous est AB = 1.

Q1. Calculez la valeur exacte puis approchée de l’arc BC

Q2. Recherchez sur Internet la longueur en cm de la coudée royale Égyptienne, par exemple celle visible au musée de Turin.

Proposez, en mètre, une valeur approchée de la coudée royale CR en utilisant π :

CR ≃ … m

Le cercle ci-dessous a comme rayon 1 :

Q3. Calculez la longueur de l’arc a pour que la somme totale des arcs de longueurs 1, π , φ et a corresponde au périmètre complet.

Q4. Vérifiez par le calcul que : φ ² = 1 + φ

Les valeurs de a et de BC (question 1) étant proches, montrez que l’on obtient l’approximation :

Vérifiez à la calculatrice (Pour aller plus loin, voir la fin du document).

Exercice 3 – Pyramide et π

On se donne un carré de côté 1 et un cercle de diamètre d :

Q1. Quel diamètre d doit avoir le cercle pour que les périmètres des 2 figures soient identiques ?

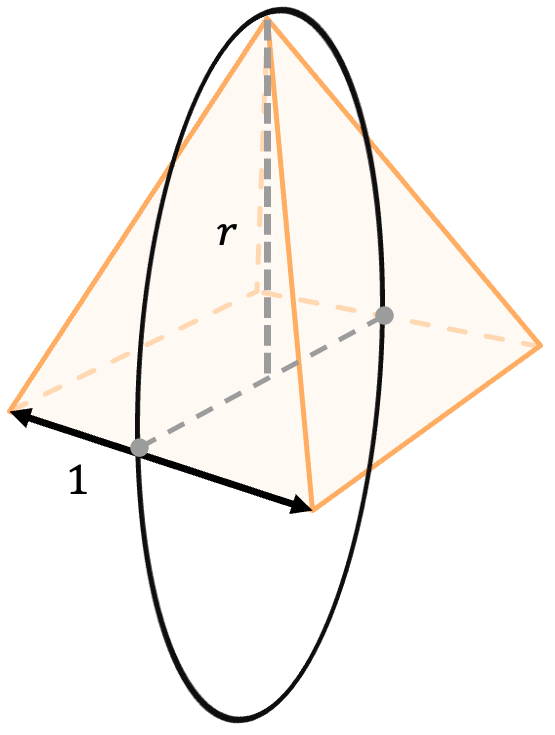
On construit maintenant une pyramide dont la base est le carré précédent et la hauteur est égale au rayon du cercle précédent :

Q2. Calculez la valeur exacte puis approchée de r

Q3. Cette valeur étant proche de la hauteur h trouvée à la question 2 de l’exercice 1, en déduire que :

Vérifiez à la calculatrice (Pour aller plus loin, voir la fin du document).

Q4. Montrez que le quotient du périmètre de la base de cette pyramide par sa hauteur est égal à 2π

Q5. Dans le cas où le carré initial a un côté égal non plus à 1 mais à la longueur 230,36 m (voir question 3 exercice 1), calculez d puis r. Comparez r à sa valeur réelle. Vérifiez que le quotient du périmètre de la base de la pyramide de Khéops divisé par sa hauteur est effectivement un nombre proche de 2π

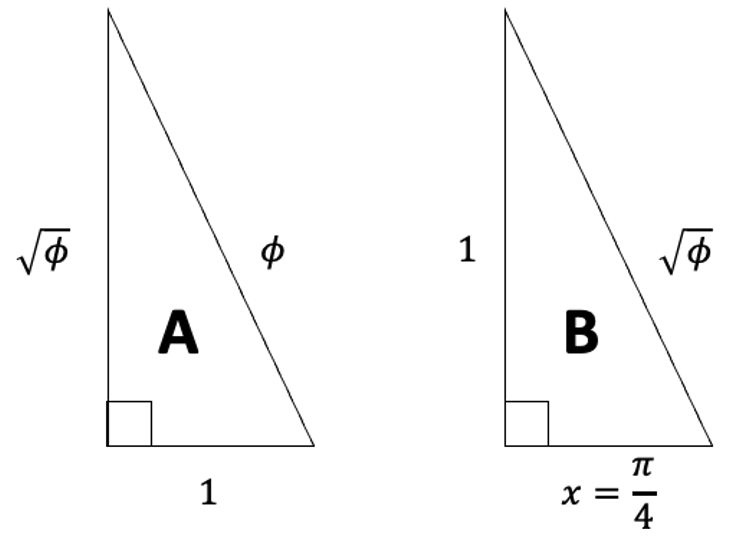
Vrais et faux triangles rectangles

Q1. Montrez que le A est bien un triangle rectangle

Q2. Montrez que le B n’est pas un triangle rectangle

Q3. Trouvez la valeur de x pour que B soit un triangle rectangle. Vérifiez à la calculatrice que cette valeur est assez proche de π / 4.

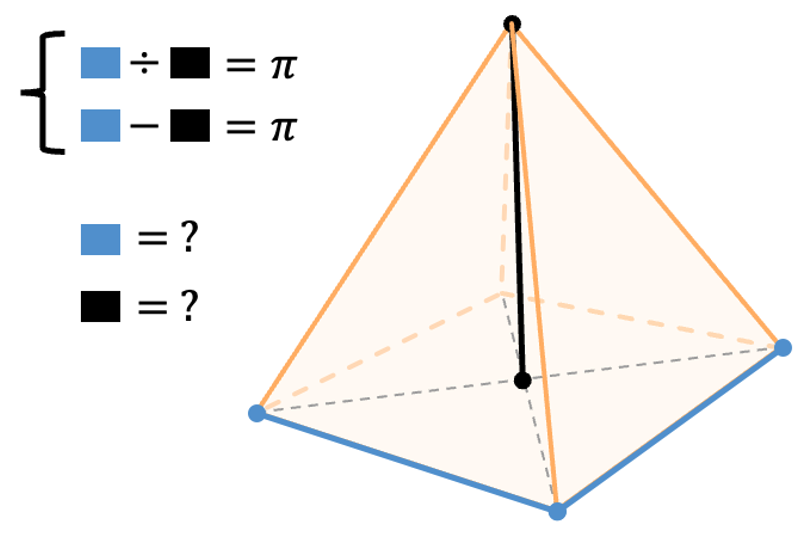
Exercice 4 – Système d’équations

Q1. Trouvez les longueurs (en bleu et en noir) telles que :

Q2. Quelles valeurs doit-on mettre dans la partie droite du système d’équations si on multiplie les longueurs en bleu et en noir trouvées précédemment par un coefficient k ?

Q3. Pour quelle valeur de k les dimensions de la pyramide de Khéops vérifient-elles (à peu près) ce système ?

Fractions continues

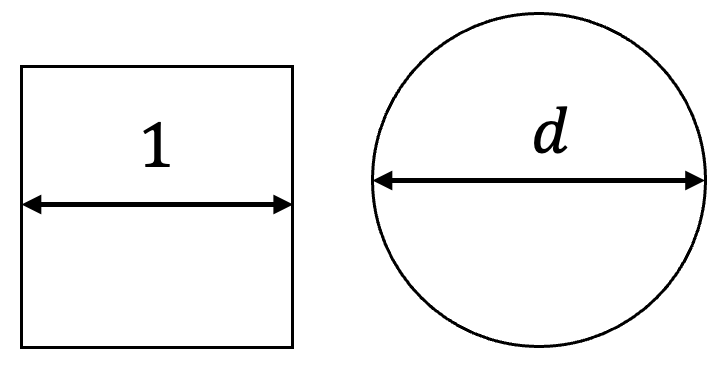
L’approximation φ ² ≃ 5π / 6 n’est pas si fantaisiste que cela puisqu’en décomposant φ ² / π en fraction continue (avec la commande dfc de Xcas par exemple), on obtient :

φ ² / π = [0, 1, 5, 2175, 2, 8, …]

C’est-à-dire qu’en première approximation, la meilleure fraction est :