Dessiner en perspective | Index de mes vidéos Youtube

Vidéo d’explication de la théorie

Explications en vidéo

Le programme principal

Copier-coller le programme ci-dessous sur cette page : https://geogebra.org/python/index.html

J’ai ajouté 2 paramètres, cx et cy, qui permettent d’étirer les valeurs numériques horizontalement et verticalement. Par exemple si vous avez dessiné un cube de largeur 1 cm sur votre plan et que vous voulez une taille 8 cm en perspective, utilisez cx = cy = 8. Vous pouvez mettre des valeurs différentes pour déformer le résultat.


pf, h = 4, 4

cx, cy = 1, 1

V = Point(0, h)

def drte(*pts):
    (xa, ya), (xb, yb) = pts
    return (yb - ya, xa - xb, xa * yb - xb * ya)

def persp(xyz):
    x, y, z = xyz
    pt1 = solve22(drte((x, y), (x + 1, y - 1)), (0, 1, 0))
    pt2 = solve22(drte((x, y), (x - 1, y - 1)), (0, 1, 0))
    if z != h:
        pt1[1] += z
        pt2[1] += z
    sol = solve22(drte(pt1, (-pf, h)), drte(pt2, (pf, h)))
    if z == h:
        return sol[0], h
    else:
        return sol

def solve22(*eq):
    (a, b, e), (c, d, f) = eq
    det = a * d - b * c
    if det != 0:
        x = (e * d - b * f) / det
        y = (a * f - e * c) / det
    return [cx * x, cy * y]

def poly(p, coul = 'black'):
    print('-' * 20)
    i = 0
    res = []
    for (x, y, z) in p:
        Z = Point(*persp((x, y, z)), is_visible = False)
        print(Z)
        res.append(Z)
    A = Polygon(res)
    A.color = coul

# Exemple : Représentation d'un plan

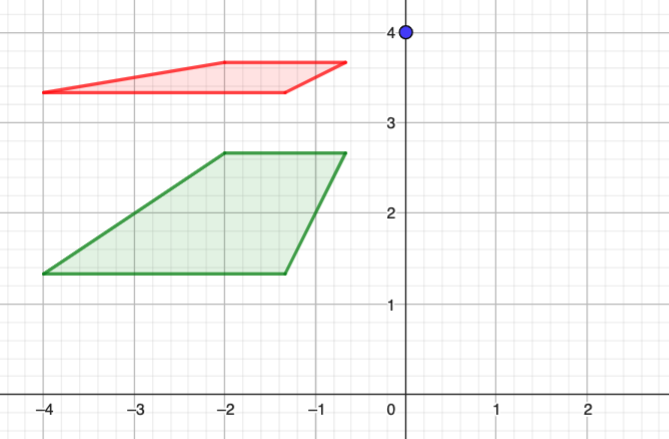
plan1 = [(-6, 2, 0),(-2, 2, 0), (-2, 8, 0), (-6, 8, 0)]
plan2 = [(-6, 2, 3),(-2, 2, 3), (-2, 8, 3), (-6, 8, 3)]

poly(plan1, 'green')
poly(plan2, 'red')

Remarque : Les calculs des coordonnées des points pt1 et pt2 ont été faits en utilisant notre fonction solve22 mais bien entendu un calcul direct était possible ! Vous pourrez montrer que la droite passant par les points A(x_A, y_A) et B(x_A + 1, y_A – 1) coupe l’axe des abscisses en x_A + y_A. De même, la droite passant par A(x_A, y_A) et B(x_A – 1, y_A – 1) coupe l’axe des abscisses en x_A – y_A. La simplification est alors :

# Ces 2 lignes :
    
pt1 = solve22(drte((x, y), (x + 1, y - 1)), (0, 1, 0))
pt2 = solve22(drte((x, y), (x - 1, y - 1)), (0, 1, 0))

# deviennent :

pt1 = [x + y, 0]
pt2 = [x - y, 0]

Programme pour les TI-82, 83…

Vous pouvez changer les valeurs du point de fuite (noté P) et de la hauteur H

Voici le programme à taper ou à télécharger.

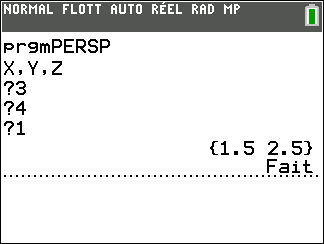
PRGM PERSP

4→P:4→H:1→S
Disp "X,Y,Z
Input X
Input Y
Input Z
0→U
If Z≠H:Z→U
H-U→A:X+Y+P→B:UP+H(X+Y→E
H-U→C:X-Y-P→D
UP+H(X-Y→F:AD-BC→G
{ED-BF,AF-EC→L₂
If Z=H:GH→L₂(2
Disp round(SL₂/G,2

Utilisation :

- Lancez le programme PERSP
- Entrez les coordonnées X, Y et Z une par une
- Les coordonnées de sa projection s'affichent
- ENTER pour entrer de nouvelles coordonnées

Projection du point (3, 4, 1) vers le point (1.5 , 2.5)

Représentation point par point en utilisant une TI-83 avec les paramètres 15→P:15→H:2→S

Autre représentation à la main en changeant point de fuite, hauteur et échelle

Exemples

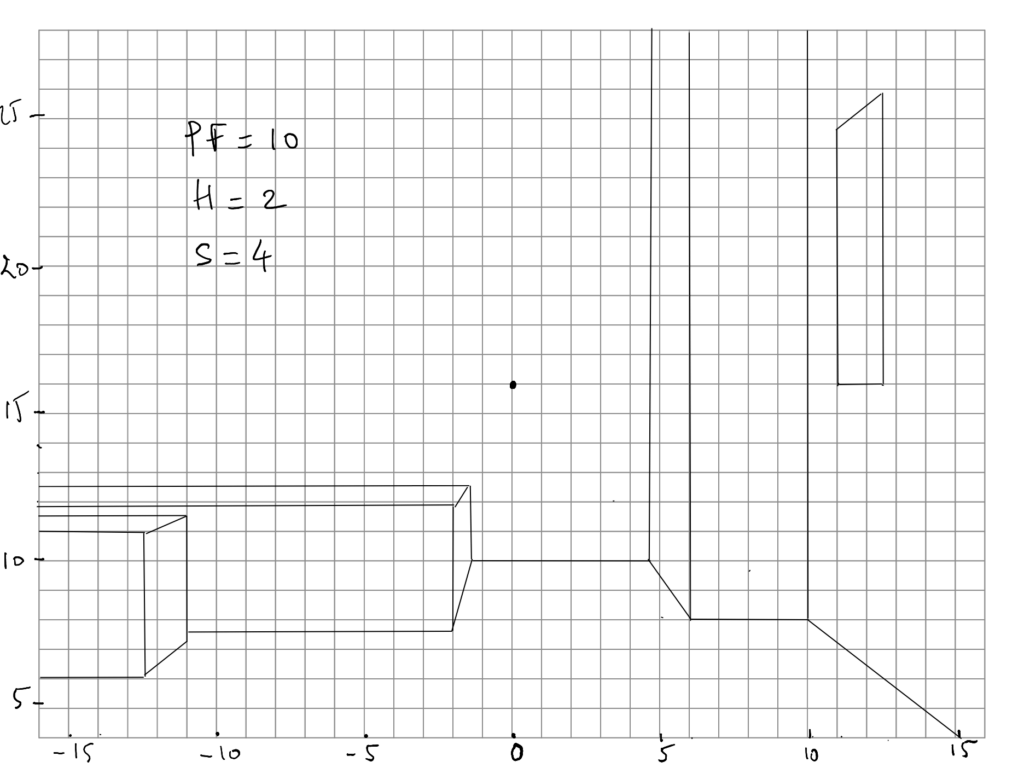
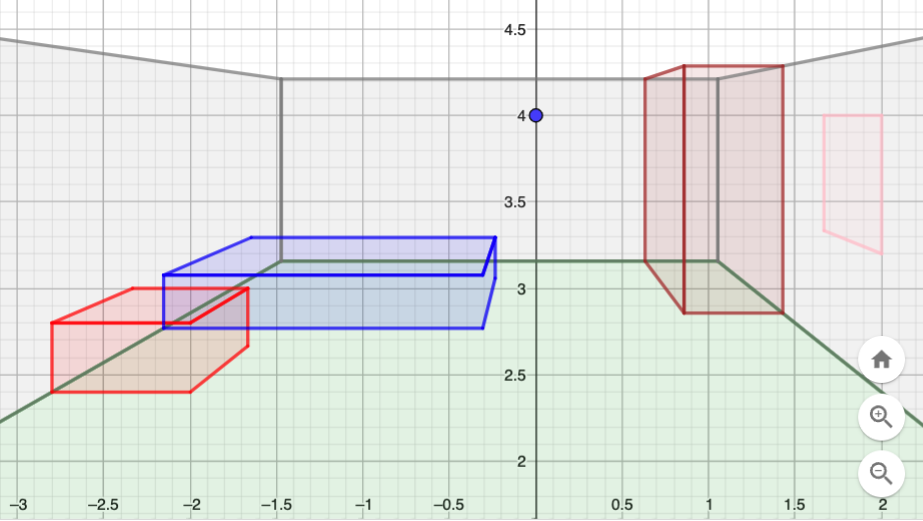
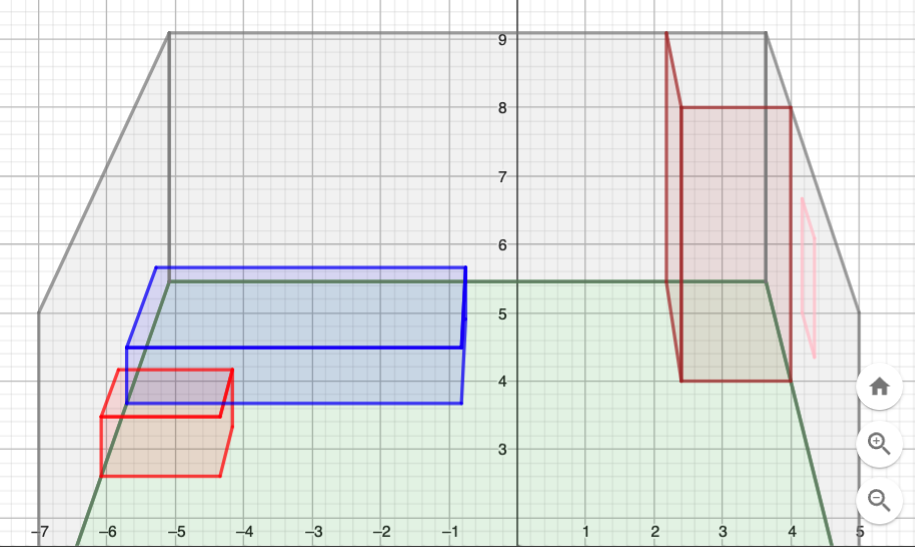
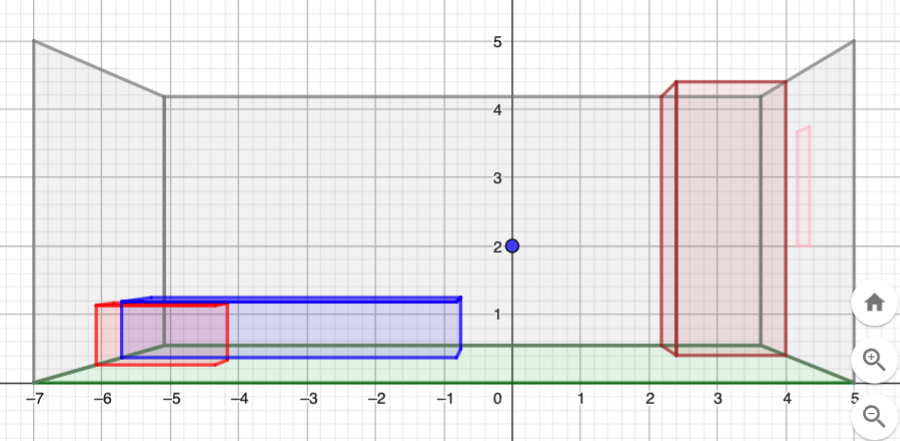
La chambre

pf, h = 4, 4

V = Point(0, h)

sol = (-7, 0, 0), (5, 0, 0), (5, 15, 0), (-7, 15, 0)
fond = (-7, 15, 0), (-7, 15, 5), (5, 15, 5), (5, 15, 0)
gauche = (-7, 0, 0), (-7, 15, 0), (-7, 15, 5), (-7, 0, 5)
droite = (5, 0, 0), (5, 15, 0), (5, 15, 5), (5, 0, 5)
chevet_cotes = (-7, 6, 0), (-5, 6, 0), (-5, 8, 0), (-5, 8, 1), (-5, 6, 1), (-7, 6, 1)
chevet_haut = (-7, 6, 1), (-7, 8, 1), (-5, 8, 1), (-5, 6, 1)
lit_cotes = (-7, 9, 0), (-1, 9, 0), (-1, 13, 0), (-1, 13, 1), (-1, 9, 1), (-7, 9, 1)
lit_haut = (-7, 9, 1), (-1, 9, 1), (-1, 13, 1), (-7, 13, 1)
armoire_cotes = (3, 10, 0), (5, 10, 0), (5, 10, 5), (3, 10, 5)
armoire_face = (3, 10, 0), (3, 15, 0), (3, 15, 5), (3, 10, 5)
cadre = (5, 6, 2), (5, 8, 2), (5, 8, 4), (5, 6, 4)

def drte(*pts):
    (xa, ya), (xb, yb) = pts
    return (yb - ya, xa - xb, xa * yb - xb * ya)

def persp(xyz):
    x, y, z = xyz
    pt1 = solve22(drte((x, y), (x + 1, y - 1)), (0, 1, 0))
    pt2 = solve22(drte((x, y), (x - 1, y - 1)), (0, 1, 0))
    if z != h:
        pt1[1] += z
        pt2[1] += z
    sol = solve22(drte(pt1, (-pf, h)), drte(pt2, (pf, h)))
    if z == h:
        return sol[0], h
    else:
        return sol

def solve22(*eq):
    (a, b, e), (c, d, f) = eq
    det = a * d - b * c
    if det != 0:
        x = (e * d - b * f) / det
        y = (a * f - e * c) / det
    return [x, y]

def poly(p, coul = 'black'):
    print('-' * 20)
    res = []
    for (x, y, z) in p:
        Z = Point(*persp((x, y, z)), is_visible = False)
        print(Z)
        res.append(Z)
    A = Polygon(res)
    A.color = coul

poly(sol, 'green')
poly(fond, 'grey')
poly(gauche, 'grey')
poly(droite, 'grey')
poly(chevet_cotes, 'red')
poly(chevet_haut, 'red')
poly(lit_cotes, 'blue')
poly(lit_haut, 'blue')
poly(armoire_cotes, 'brown')
poly(armoire_face, 'brown')
poly(cadre, 'pink')

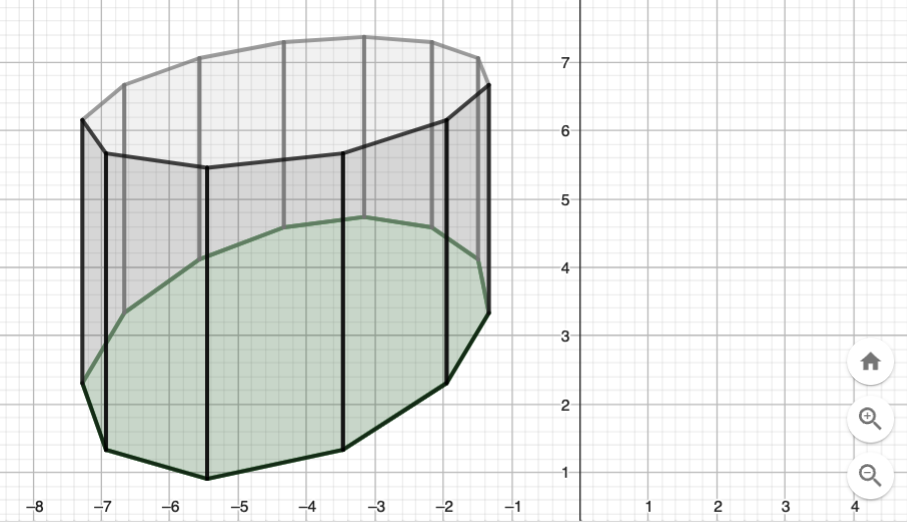
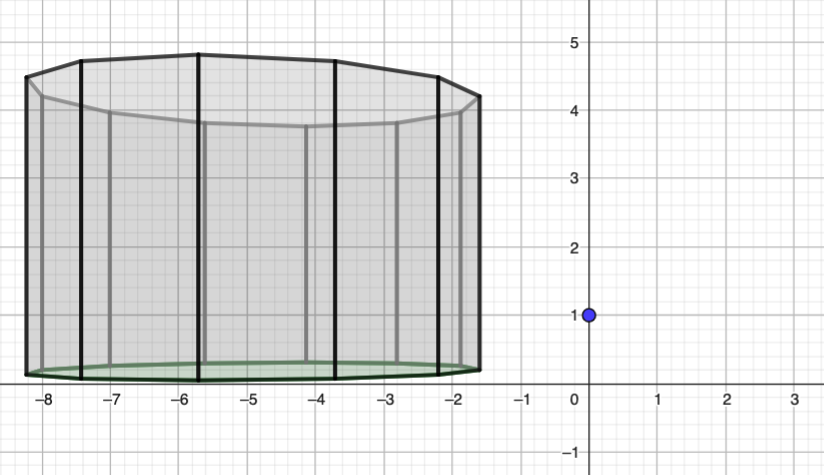
pf, h = 15, 1 sur la calculatrice NUMWORKS

Prisme dodécagonal

from math import *

pf, h = 10, 10

V = Point(0, h)

haut, bas = [], []

n = 12
for i in range(n):
    x , y = -6+4 * cos(2 * i * pi / n), 5 + 4 * sin(2 * i * pi / n)
    haut.append((x,y,5))
    bas.append((x,y,0))
    
def drte(*pts):
    (xa, ya), (xb, yb) = pts
    return (yb - ya, xa - xb, xa * yb - xb * ya)

def persp(xyz):
    x, y, z = xyz
    pt1 = solve22(drte((x, y), (x + 1, y - 1)), (0, 1, 0))
    pt2 = solve22(drte((x, y), (x - 1, y - 1)), (0, 1, 0))
    if z != h:
        pt1[1] += z
        pt2[1] += z
    sol = solve22(drte(pt1, (-pf, h)), drte(pt2, (pf, h)))
    if z == h:
        return sol[0], h
    else:
        return sol

def solve22(*eq):
    (a, b, e), (c, d, f) = eq
    det = a * d - b * c
    if det != 0:
        x = (e * d - b * f) / det
        y = (a * f - e * c) / det
    return [x, y]

def poly(p, coul = 'black'):
    print('-' * 20)
    i = 0
    res = []
    for (x, y, z) in p:
        Z = Point(*persp((x, y, z)), is_visible = False)
        print(Z)
        res.append(Z)
    A = Polygon(res, line_thickness=6)
    A.color = coul
    
poly(bas,'green')

for i in range(n):
    poly([bas[i],haut[i],haut[(i+1)%n],bas[(i+1)%n]], 'grey' if i <= n/2 else 'black')

Version pour la calculatrice NUMWORKS : https://my.numworks.com/python/schraf/prisme

Exemple plus avancé

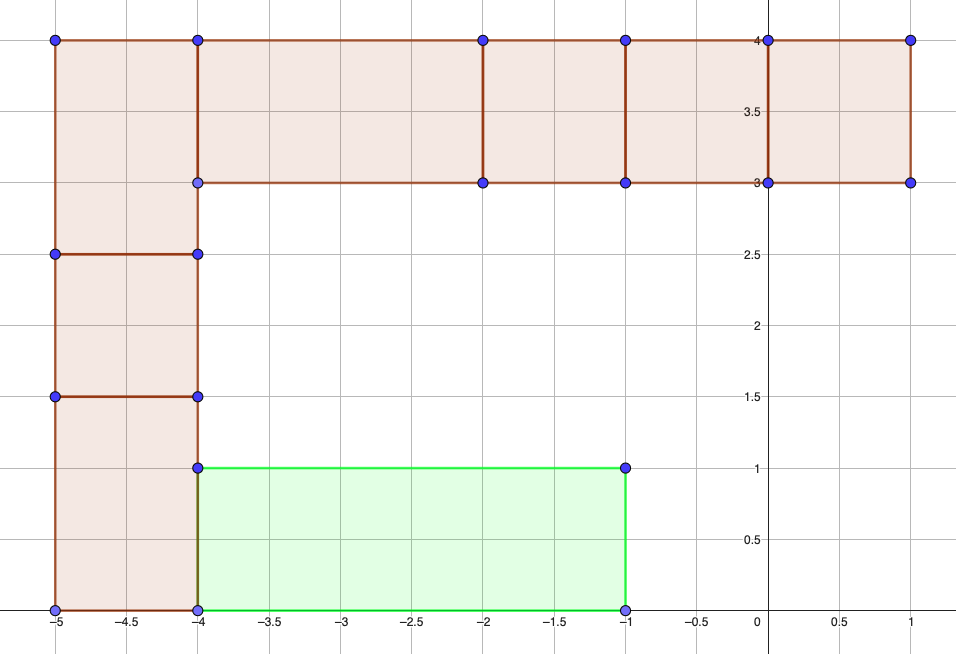
Voici le plan (vue du dessus) d’une cuisine :

Supposons que les meubles fassent 1 de hauteur. Pour mémoriser un meuble, on peut regarder uniquement ses coordonnées en diagonale, par exemple pour le meuble du bas en vert, sa diagonale est (-4,0,0) et (-1,1,1), le 0 parce que le meuble touche le sol et 1 qui correspond à sa hauteur.

On peut alors créer une fonction box qui affichera les 5 ou 6 faces (on peut s’épargner la face inférieure). Voir code plus loin.

On peut également ajouter une fonction de rotation pour avoir une vue sous différents angles horizontalement.

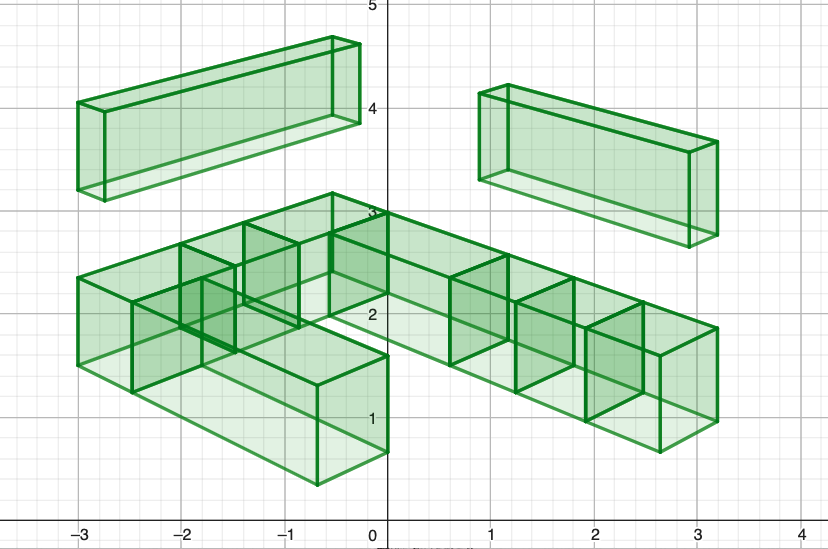
Voici le script final avec 10 meubles :

from math import *
pf, h = 20, 10

cx, cy = 1, 1

# Les faces d'un meuble

faces = ((0,0,0),(0,0,1),(0,1,1),(0,1,0)), ((0,0,0),(0,0,1),(1,0,1),(1,0,0)),\
        ((1,0,0),(1,0,1),(1,1,1),(1,1,0)), ((0,0,1),(0,1,1),(1,1,1),(1,0,1)),\
        ((0,1,0),(0,1,1),(1,1,1),(1,1,0))

# Les meubles
o1 = (-4,0,0), (-1,1,1)
o2 = (-5,0,0), (-4,1.5,1)
o3 = (-5,1.5,0), (-4,2.5,1)
o4 = (-5,2.5,0), (-4,4,1)
o5 = (-4,3,0), (-2,4,1)
o6 = (-2,3,0), (-1,4,1)
o7 = (-1,3,0), (0,4,1)
o8 = (0,3,0), (1,4,1)
o9 = (-5,0,2), (-4.5,4,3)
o10 = (-2,3.5,2), (1,4,3)

# Matrice de rotation
def rotate(x,y,angle):
  xr = x*cos(angle) - y*sin(angle)
  yr = x*sin(angle) + y*cos(angle)
  return (xr,yr)

# Affichage d'un meuble
def box(ob):
    for f in faces:
     s = []    
     for (i,j,k) in f:
         a,b = rotate(ob[i][0],ob[j][1], radians(-45))
         s.append((a,b,ob[k][2]))
     poly(s, 'green')     
        
def drte(*pts):
    (xa, ya), (xb, yb) = pts
    return (yb - ya, xa - xb, xa * yb - xb * ya)

def persp(xyz):
    x, y, z = xyz
    pt1 = solve22(drte((x, y), (x + 1, y - 1)), (0, 1, 0))
    pt2 = solve22(drte((x, y), (x - 1, y - 1)), (0, 1, 0))
    if z != h:
        pt1[1] += z
        pt2[1] += z
    sol = solve22(drte(pt1, (-pf, h)), drte(pt2, (pf, h)))
    if z == h:
        return cx * sol[0], cy * h
    else:
        return cx * sol[0], cy * sol[1]

def solve22(*eq):
    (a, b, e), (c, d, f) = eq
    det = a * d - b * c
    if det != 0:
        x = (e * d - b * f) / det
        y = (a * f - e * c) / det
    return [x, y]

def poly(p, coul = 'black'):
    print('-' * 20)
    res = []
    for (x, y, z) in p:
        Z = Point(*persp((x, y, z)), is_visible = False)
        print(Z)
        res.append(Z)
    A = Polygon(res)
    A.color = coul

for ob in (o1,o2,o3,o4,o5,o6,o7,o8,o9,o10): box(ob)