Créez en 1971 par Lorinda Cherry et Robert Morris, dc est une calculatrice RPN (Notation Polonaise Inverse) à précision arbitraire. Découvrons ensemble quelques unes de ses fonctionnalités.

Si vous n’êtes pas sous Windows, lancez un Terminal puis tapez dc, sinon utilisez la version en ligne (tapez les commandes dans la zone Code.

Calculs élémentaires

% dc                 # Lancement de l'outil
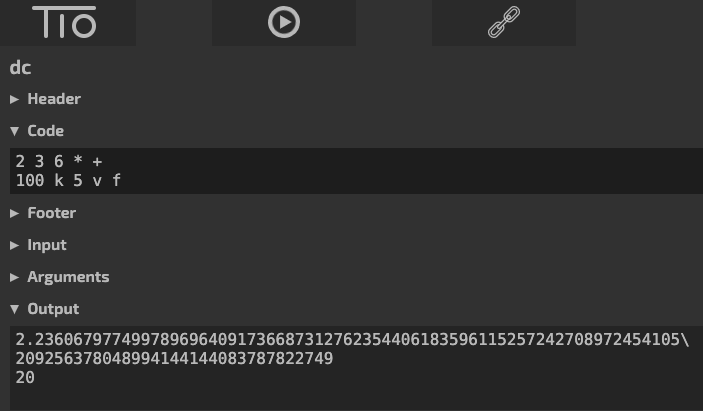
>>> 2 3 6 * + p      # 2 + 3 * 6 = 20
20                   # p : afficher le sommet de la pile

>>> _7 _8 * p        # Ecriture des nombres négatifs
56

>>> 100 k 5 v f
2.236067977499789696409173668731276235440618359611525724270897245410\
5209256378048994144144083787822749
56
20

# 100 k : on veut une précision avec 100 décimales
# 5 v : racine carrée de 5
# f : voir la pile complète (on retrouve donc les 20 et 56 précédents)

>>> c 2023 sa    # c : effacer toute la pile et s(TO) 2023 dans registre 'a'
>>> f            # f : s(TO) supprime l'élément de la pile -> pile vide

>>> la f         # l(OAD) le registre 'a' et affiche la pile
2023

dc n’a pas de fonctions mathématiques avancées (trigo, log…) contrairement à bc mais qui travaille en mode algébrique.

changement de bases

On peut passer facilement d’une base à une autre. Par exemple, je veux taper des valeurs en binaire et connaitre leurs traductions en base 10 :

>>> 2i      # les valeurs entrées (input) seront en base 2
>>> c 10 111 1010 1111111111 f 
1023
10
7
2

# Pour revenir à une saisie en base 10 il faut taper 1010i car 10 en décimal s'écrit 1010 en binaire. Et on veut que les sorties soient en base 16 :

>>> 1010i 16o       # Entrée en base 10 et sortie (output) en base 16
>>> c 3 14 159 265358 f
40C8E
9F
E
3  

Une autre solution est de taper : Ai Ao (« A » correspondant à la base 10)

Création de macros

Créons 2 macros, la première divise un nombre par 2, la seconde le multiplie par 3 et ajoute 1.

>>> [2/]sp           # programme 2 / enregistré dans 'p'
>>> [3*1+]si         # programme 3 * 1 + enregistré dans 'i'
>>> c 27 li x p      # on efface la pile, ajout de 27 et exécution de 'i'
82                   # 27 * 3 + 1 = 82

>>> 27 lpxp          # Les espaces sont optionnels ! 27 lp x p
13                   # programme 'p' avec 27 et affichage top de la pile

Ajouter des commentaires

Vous pouvez utiliser # à la fin d’une ligne ou écrire un commentaire entre [ ] puis le mettre dans un registre « bidon » :

>>> 16 25 # ajout 2 nombres sur la pile
>>> 16 25 [ajout de 2 nombres sur la pile]sz

Commandes sur la pile

On a déjà vu c pour effacer toute la pile et p pour afficher l’élément au top de la pile sans le supprimer.

Il y a également r pour inverser (SWAP) les 2 éléments au top de la pile et d pour dupliquer (DUP) l’élément qui est au top de la pile.

R permet d’effacer l’élément au top de la pile (DROP) :

>>> 45 78 89 f
89
78
45
>>> R f
78
45

Exercices corrigés

Les exercices et corrigés sont de mon cru, il est donc probable que vous trouviez des solutions meilleures ou plus élégantes.

Expliquez le déroulement du programme nommé ‘.’ (les noms des registres ne se limitent pas aux lettres de l’alphabet !)

>>> [dsarla]s.
>>> 4 8 l.xf

Corrigé : Le programme ‘.’ s’écrit [d sa r la] en version éclatée. C’est-à-dire dupliquer le top de la pile, le mémoriser dans le registre ‘a’ (donc la version dupliquée disparait de la pile), inverser les 2 éléments et mettre ‘a’ sur la pile.

On aura donc successivement : 4 8 -d-> 4 8 8 -sa-> 4 8 et 8 dans ‘a’ -r-> 8 4 -la-> 8 4 8

Vous avez peut-être reconnue la commande OVER qui permet de passer de x y à y x y

Que fait ce programme nommé ‘:’ ?

>>> [sndlnrln]s:
>>> 4 8 l:xf

Corrigé :

4 8 -sn-> 4 et 8 dans registre ‘n’ -d-> 4 4 -ln-> 4 4 8 -r-> 4 8 4 -ln-> 4 8 4 8

C’était une traduction de la commande DUP2 qui duplique les 2 éléments au top de la pile : x y -> x y x y

Que fait ce programme nommé ‘r’ ?

>>> [sasblarlb]sr
>>> c 4 8 12 f
>>> c 4 8 12 lrxf

Corrigé :

>>> c 4 8 12 f
12
8
4

En appliquant la macro ‘r’ aux 3 éléments :

4 8 12 -sa-> 4 8 et 12 dans ‘a’ -sb-> 4 et 8 dans ‘b’ -la-> 4 12 -r-> 12 4 -lb->12 4 8

>>> c 4 8 12 lrxf
8
4
12

On reconnait ROT qui permet de passer de x y z à z x y.

Les boucles

Créer une boucle consiste à répéter une macro un certain nombre de fois. Ce nombre étant géré par un test, en voici quelques uns qui lanceront ou non le programme ‘r’ :

>>> [2023]sr      # le programme 'r' met 2023 sur la pile
>>> c 1 1 =r f    # comme 1=1 le programme est exécuté
2023
>>> c 1 2 =r f    # comme 1≠2 le programme n'est pas exécuté

>>> c 1 2 <r f    # 2 n'est pas < à 1 

>>> c 2 2 !<r f   # 2 est ≥ à 2, le programme s'exécute
2023

Exercices corrigés

Comprendre le déroulement du programme ci-dessous :

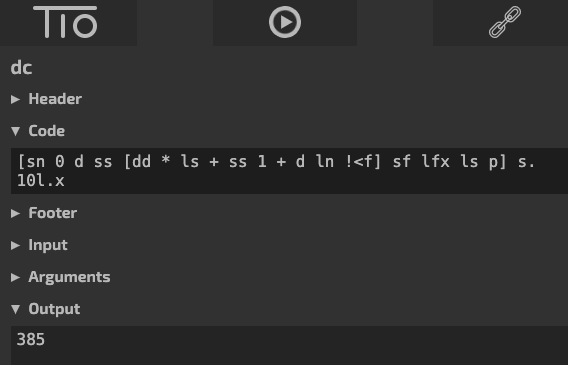
>>> [sn 0 d ss [dd * ls + ss 1 + d ln !<f] sf lfx ls p] s.
>>> 5 l.x
55
>>> 10 l.x
385

Corrigé :

sn 0 d ss : initialisation en mettant le nombre dans ‘n’ et 0 dans ‘s’ (future somme)

Avant d’entrer dans la macro ‘f’ il n’y a que 0 (compteur) sur la pile. On duplique 2 fois cette valeur, on en fait le produit (carré) que l’on ajoute à ‘s’. Le compteur augmente de 1 et on le compare à ‘n’. Si n ≥ compteur on applique à nouveau la macro ‘f’.

Tout le programme […] est mémorisé dans ‘f’ (qui disparait donc de la pile) et on applique ‘f’ à 0. Bien voir que l’on aurait pu à part définir ‘f’ et donc écrire :

>>> [dd * ls + ss 1 + d ln !<f] sf
>>> [sn 0 d ss lfx ls p] s.
>>> 10 l.x
385

# Ou inversement tout compacter :
>>> [sn0dss[dd*ls+ss1+dln!<f]sflfxlsp]s.
>>> 10 l.x
385

Le programme permet donc de calculer la somme des carrés des entiers entre 1 et N.

Que va faire ce programme ?

>>> [sndlnrln<r]s.
>>> [r]sr
>>> c 4 8 l.x f
?
?
>>> c 8 4 l.x f
?
?

Corrigé : la macro ‘.’ débute par DUP2 (duplication des 2 valeurs saisies). Plus précisément si x y sont sont sur la pile, sndlnrln donnera x y –snd-> x x -lnr-> x y x -ln-> x y x y puis on teste si y < x. Si c’est vrai alors le programme ‘r’ inverse les 2 éléments. On aura donc toujours max(x,y) au-dessus de min(x,y).

>>> c 4 8 l.x f 
8
4
>>> c 8 4 l.x f
8
4

Somme des chiffres

Ecrire un programme ‘s’ qui donne la somme des chiffres d’un entier quelconque

>>> 123 lsx
6
>>> 123456789 lsx
45

Une proposition :

>>> [[d10%r10/d0<f+]sflfxp]ss

Comprendre le programme pas à pas.

Correction : Il y a une première macro

[d 10 % r 10 / d 0 <f +] sf

# dupliquer le nombre et chercher N % 10 (N modulo 10)
# on a donc N et N%10 sur la pile
# inverser (SWAP) les 2 et faire la division par 10
# on a N%10 et N/10 sur la pile
# on duplique le top de la pile : N%10 N/10 N/10
# Si cette valeur est >0 recommencer la macro 'f'
# Par exemple avec 1234 on aura donc 4 123 au premier tour
# puis 4 3 12, ensuite 4 3 2 1 et enfin 4 3 2 1 0
# Ensuite '+' est appliqué récursivement soit 0 + 1 + 2 + 3 + 4

Version 2

>>> [[d10%r10/d0<f+]sflfxp]ss     # Version 1
>>> [?[10~rd0<f+]dsfxp]ss        # Version 2
>>> lsx        # On lance la macro 's'
?> 123         # ? : prompt
6

~ permet d’avoir le reste et le quotient en une seule fois :

>>> 123 10 ~ f
3
12

PGCD entre 2 nombres

Ecrire une macro qui à partir de 2 nombres donne leur PGCD. On pourra supposer que le 1er nombre est plus grand que le 2e :

>>> 220220 53482 # Votre macro ici
3146

Pensez à l’algorithme d’Euclide, le PGCD est le dernier reste non nul des divisions successives.

Corrigé :

>>> 220220 53482 [dsa%lard0<:]ds:x+p
3146

# d sa % : on mémorise la 2e valeur et calcul du reste
# la r : on rappelle la 2e valeur que l'on met en première position
# Ainsi, à la première étape on aura : 
# 220220 53482 -d sa-> 220220 53482 et 53482 dans registre 'a'
# 6292 -la-> 6292 53482 -r-> 53482 6292
# d 0<: Si le reste est >0 on recommence la macro ':'
# ds:x on mémorise la macro et on l'exécute
# En sortant de la boucle on a le dernier reste non nul et 0
# Pour l'exemple on aura 3146 0
# +p : on en fait la somme et on affiche le résultat

Somme de tous les éléments de la pile

Analysons cette commande :

>>> c
>>> 1 4 3 10 [+z1<+]s+l+xp
18

# On efface le contenu précédent de la pile avec 'c'
# On place 1 4 3 10 sur la pile
# On ajoute les 2 éléments au top
# 'z' permet de compter le nombre d'éléments sur la pile (ici 4)
# Comme on a fait une addition, le nombre d'éléments diminue de 1
# si ce nombre est >1 on relance la macro '+'
# l+x permet d'exécuter la macro '+' et 'p' d'afficher le résultat

Remarques : Au lieu d’écrire s+ pour stocker le programme puis l+x pour le lancer, on peut aussi écrire d s+ x ou ds+x; Ce qui signifie : dupliquer (la chaine de caractères), stocker dans ‘+’ et exécuter (‘x’).

>>> c
>>> 1 4 3 10 [+z1<+]ds+xp
18

On peut également ajouter un prompt qui va demander la liste des nombres :

>>> c?[+z1<+]ds+xp
?> 5 10 9 12
36

Sortir d’une boucle, affichage de textes

Ecrivons un programme qui teste si une année est bissextile ou non. Si une année n’est pas divisible par 4 elle n’est pas bissextile, sinon, si elle n’est pas divisible par 100 elle est bissextile (elle est donc divisible par 4 et pas par 100), sinon si elle n’est pas divisible par 400 elle n’est pas bissextile, sinon elle est bissextile !

>>> [[NON BISSEXTILE]pcq]s0     # Affiche texte, efface la pile et quitte
>>> [[BISSEXTILE]pcq]s1
>>> [d s. 4 % 0!=0 l. 100 % 0!=1 l. 400 % 0!=0 l1x] sb

>>> 2023 lbx
NON BISSEXTILE
>>> 2024 lbx
BISSEXTILE
>>> 1900 lbx
NON BISSEXTILE
>>> 2000 lbx
BISSEXTILE

Ecrire un nombre dans toutes les bases entre 2 et 16

A partir d’un nombre (2023 pour l’exemple), on voudrait voir le texte « Base » suivi d’un nombre entre 2 et 16 et à côté la traduction dans la base correspondante :

>>> [2 [[Base ]nd 10o dn[ : ]n o r p r 1 + d 16!<:] ds:x] sb
>>> 2023 lbx
Base 2 : 11111100111
Base 3 : 2202221
Base 4 : 133213
Base 5 : 31043
Base 6 : 13211
Base 7 : 5620
Base 8 : 3747
Base 9 : 2687
Base 10 : 2023
Base 11 : 157A
Base 12 : 1207
Base 13 : BC8
Base 14 : A47
Base 15 : 8ED
Base 16 : 7E7

Explications de la macro :

# [Base ]nd 10o dn[ : ]n o

# [Base ]n : Affiche "Base " sans retour à la ligne ('n')
# d : on duplique le chiffre qui sera la base
# 10o : on se met momentanément en base 10
# n[ : ]n : On affiche le chiffre sans retour à la ligne suivi de " : "
# o : on impose la sortie dans la base voulue

# r : On inverse la base et le nombre à transformer
# p : on imprime ce nombre
# r : On inverse à nouveau base et nombre

# 1 + d 16!<: La base augmente de 1 et on recommence si elle est ≤16

Factorisation d’un entier

Ecrire un programme ‘f’ qui factorise un entier, par exemple :

>>> 178307670177 lfx
3
3
7
13
17
23
37
101
149

Voici une version qui n’utilise pas beaucoup la pile mais plutôt des registres :

[[lnlip/sn]s.[li1+si]s:[lnli%d0=.d0!=:ln1<;]s;sn2sil;x]sf

Essayez de comprendre le déroulement…

Corrigé : Il y a plusieurs macros que nous allons décomposer :

[ln li p / sn] s.

# on rappelle 'n' et 'i', cette dernière est affichée
# puis on effectue la division et le résultat est stocké dans 'n'
# cette macro '.' actualise 'n' par 'n/i' lorsque 'i' est un diviseur

[li 1 + si] s:
# Incrémentation de 'i'

[ln li % d 0=. d 0!=: ln 1<;] s;

# on cherche le reste de la division de 'n' par 'i'
# si le reste est nul on applique la macro '.'
# sinon on augmente 'i' de 1 (macro ':')
# Tant que n > 1 on refait la macro ';'

sn 2 si l;x

# Initialisation de 'n' et lancement de la macro 'f'

L’idée est donc de tester la division de ‘n’ par ‘i’ en commençant par i = 2. Tant que la division tombe juste on affiche ‘i’ et on met à jour ‘n’ en le remplaçant par ‘n / i’. Sinon on augmente ‘i’ de 1 et on arrête lorsque n = 1.

Remarque : J’ai trouvé cet autre programme page 308 dans Advanced Bash-Scripting :

>>> 124 [p]s2[lip/dli%0=1dvsr]s12sid2%0=13sidvsr[dli%0=1lrli2+dsi!>.]ds.xd1<2
2
2
31

Conjecture de Syracuse

Programmez la conjecture de Syracuse (Collatz) : Partir d’un entier N non nul, le diviser par 2 s’il est pair, le multiplier par 3 et ajouter 1 s’il est impair. Répéter jusqu’à obtenir 1. Quel maximum a été atteint et combien d’itérations aura-t-il fallu faire ?

Exemple : N = 27 -> 82 -> 41 -> 124 -> 62 -> … -> 9232 -> … 4 -> 2 -> 1

Le maximum est 9232 et il faut 111 itérations avant d’arriver à 1.

Une solution :

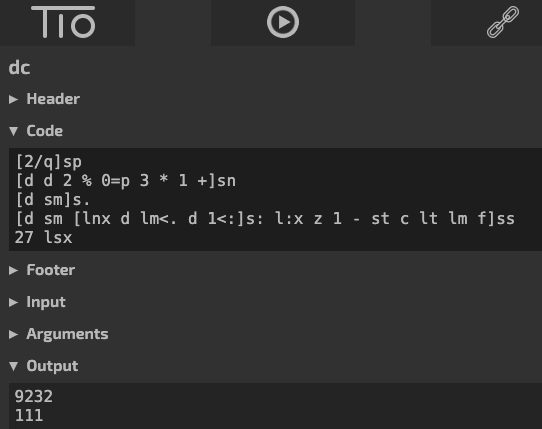
>>> [2/q]sp
>>> [d d 2 % 0=p 3 * 1 +]sn
>>> [d sm]s.
>>> [c? d sm [lnx d lm<. d 1<:]s: l:x z 1 - st c lt lm f]ss

>>> lsx
?> 27
9232      # Max atteint
111       # Temps de vol (nb d'itérations)

>>> lsx
?> 6171
975400
261

>>> lsx
?> 8400511
159424614880
685

>>> lsx
?> 12345678901234567890123
55555555055555555505556
575

Explications :

[2/q]sp : diviser par 2 et quitter la macro appelante
[d d 2 % 0=p 3 * 1 +] sn : si nombre est pair, lancer programme 'p'
sinon multiplier par 3 + 1 (le 'q' de la macro 'p' permet donc
de sortir de la macro 'n' quand le nombre est pair)
[d sm]s. : La macro '.' écrase le max avec la valeur courante

c? d sm : On efface la pile, demande de la valeur initiale et
on la met dans le max.

[lnx d lm<. d 1<:]s: On applique la macro 'n' qui donne le nombre suivant (et laisse le précédent sur la pile), si max est < à la valeur courante on exécute
la macro '.', si valeur actuelle > 1 on recommence.

l:x z 1 - st c lt lm f : On exécute la macro ':', à la sortie on récupère le nb d'éléments de la pile (-1), on efface la pile et on affiche le temps de vol
et le max.