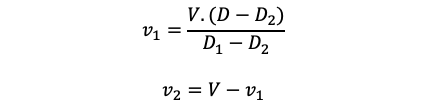Challenges 2023 pour calculatrices HP | Index de mes vidéos Youtube

Voici les challenges que j’ai proposés sur Twitter et Facebook (HP Calculator Fan Club), à programmer sur calculatrices HP.

Je mets des solutions en RPL (pour HP 48-49-50 g) et parfois pour d’autres machines (HP 12C, HP 35S, HP Prime…). J’ajoute des solutions en Python et APL.

Enoncés et corrigés

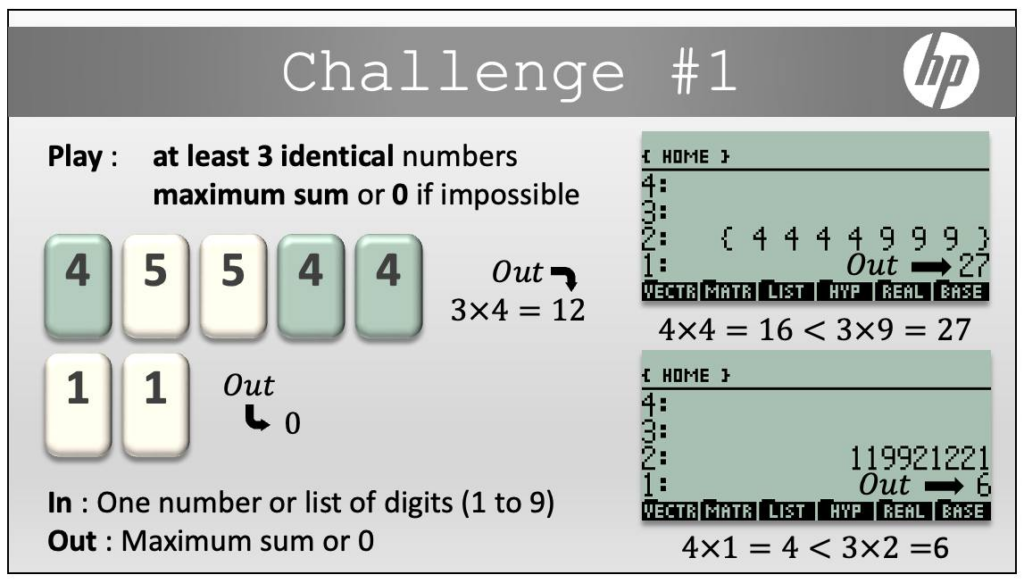
CHALLENGE #1

=== HP 48+ - Eric Schraf ===

« 0 + →t 		' t = {0, numbers...}
« 0 1 9 FOR i	        ' m = 0 ; for i = 1 to 9
  t i - NOT		' t == i ? -> {True False...}
  ΣLIST			' n = sum({True False...})
  DUP 2 > * i *		' p = n * i * (n > 2)
  MAX NEXT » »	        ' m = max(p, m)
'CH01 STO

1: {4 4 4 9 9 9}
VAR CH01
1: 27

=== Version Python - Eric Schraf ===

def ch01(arr):
  maxi = 0
  for v in set(arr): 
    n = arr.count(v)
    if n > 2: maxi = max(maxi, n * v)
  return maxi

>> ch01([4,4,4,9,9,9])
27
>> ch01([1,1,9,9,2,1,2,2,1])
6

=== Version APL - Eric Schraf ===

      ⌈/, {⍺ × (n > 2) × n ← ⍴⍵} ⌸ 4 4 4 4 9 9 9
27
      ⌈/, {⍺ × (n > 2) × n ← ⍴⍵} ⌸ 1 1 9 9 2 1 2 2 1
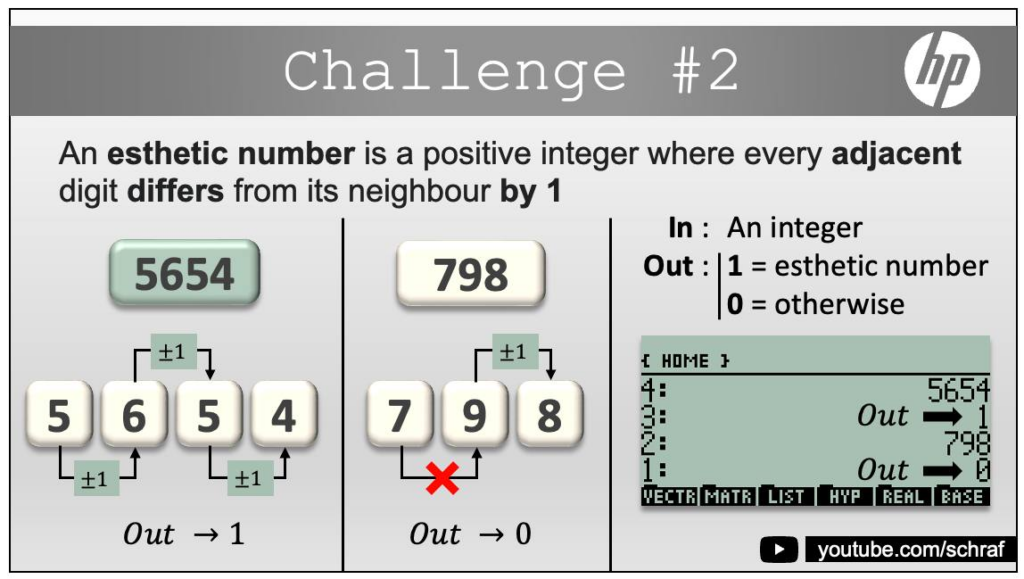
6

CHALLENGE #2

=== HP 48+ - Eric Schraf ===

« {} SWAP WHILE DUP 0 >   ' Transformation nombre en liste
REPEAT DUP 10 MOD ROT +   ' Ajout de l'unité à la liste
SWAP 10 / IP END          ' On passe à l'unité suivante
DROP ΔLIST                ' Différences successives
ABS 1 >                   ' Test si certains dépassent 1
ΣLIST NOT                 ' On les compte : 1 si aucun > 1
»
'CH02 STO

1: 5654
VAR CH02
1: 1
1: 798
CH02
1: 0

=== HP Prime - Uwe Sauerland ===

EXPORT ch02(n)
BEGIN
  LOCAL k, s := STRING(n);
  FOR k FROM 1 TO DIM(s) - 1 DO
    IF ABS(EXPR(s[k, 1]) - EXPR(s[k + 1, 1])) ≠ 1 THEN
      RETURN 0;
    END;
  END;
  RETURN 1;
END;

=== Version APL - Eric Schraf ===

      ch02 ← ∧/ 1 = ∘ | 2 -/ (⍎¨ ⍕)

      ch02 '5654'
1
      ch02 '798'
0
      ch02 '12345654565432123'
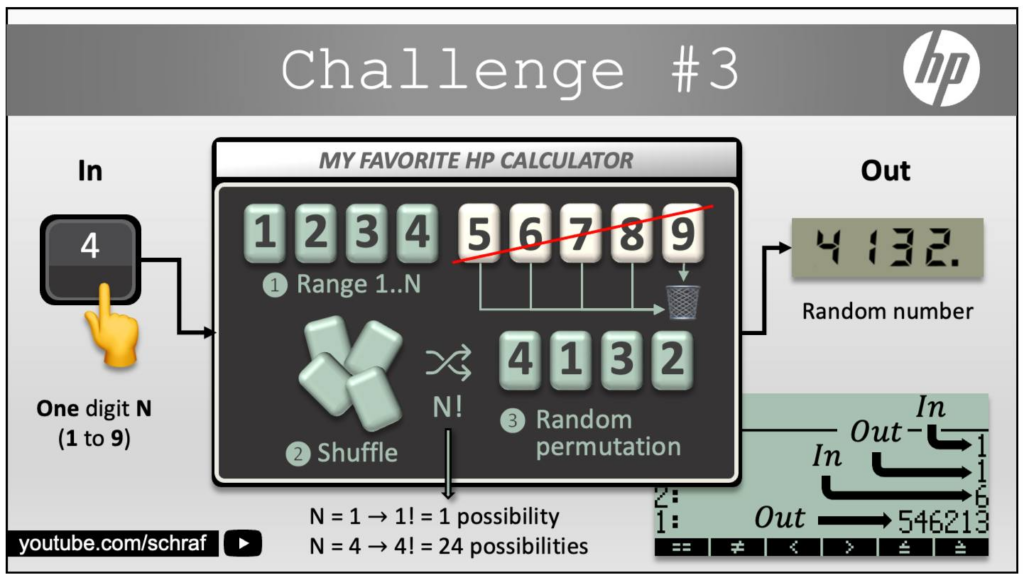
1

CHALLENGE #3

=== HP48+ - Eric Schraf ===

« "123456789" → t s          ' t = longueur voulue
« s t 1 FOR j                ' for j = t to 1 step -1
j RAND * CEIL DUP 'K' STO    ' k = randint(1, j+1) 
DUP SUB 'V' STO              ' Echanger s[k] et s[j]
s K s j j SUB REPL           
j V REPL
DUP 's' STO -1 STEP          ' next 
t SUB OBJ→                   ' transformation chaine en nombre
» »

=== HP PRIME - Eric Schraf ===

ch03:= X → EXPR(cat(randperm(X)))

ch03(5) --> 52143
ch03(1) --> 1

=== APL - Eric Schraf ===

      ch03 ← 10 ⊥ ?⍨

      ch03 5
23415
      ch03 1
1
      ch03 9
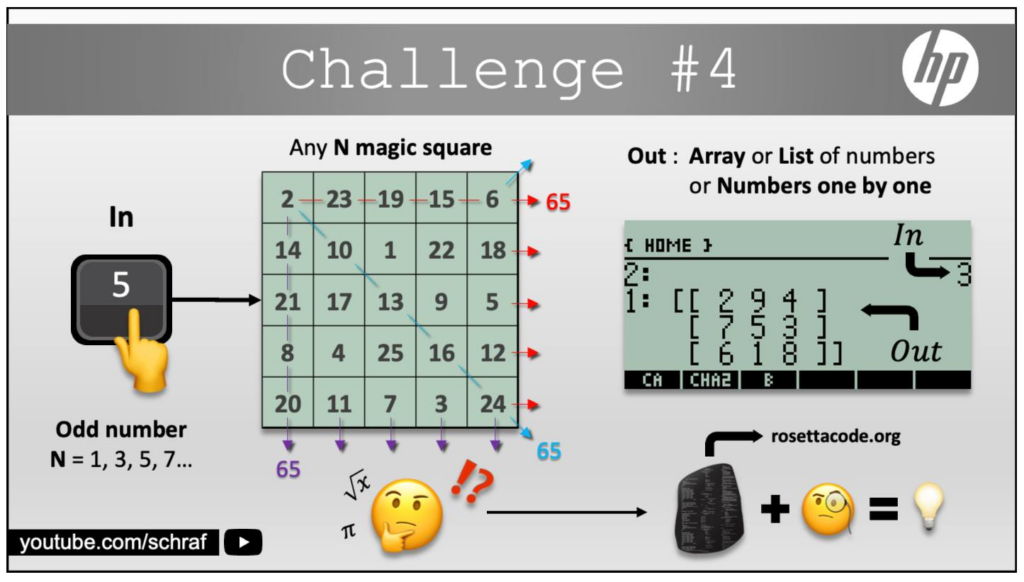
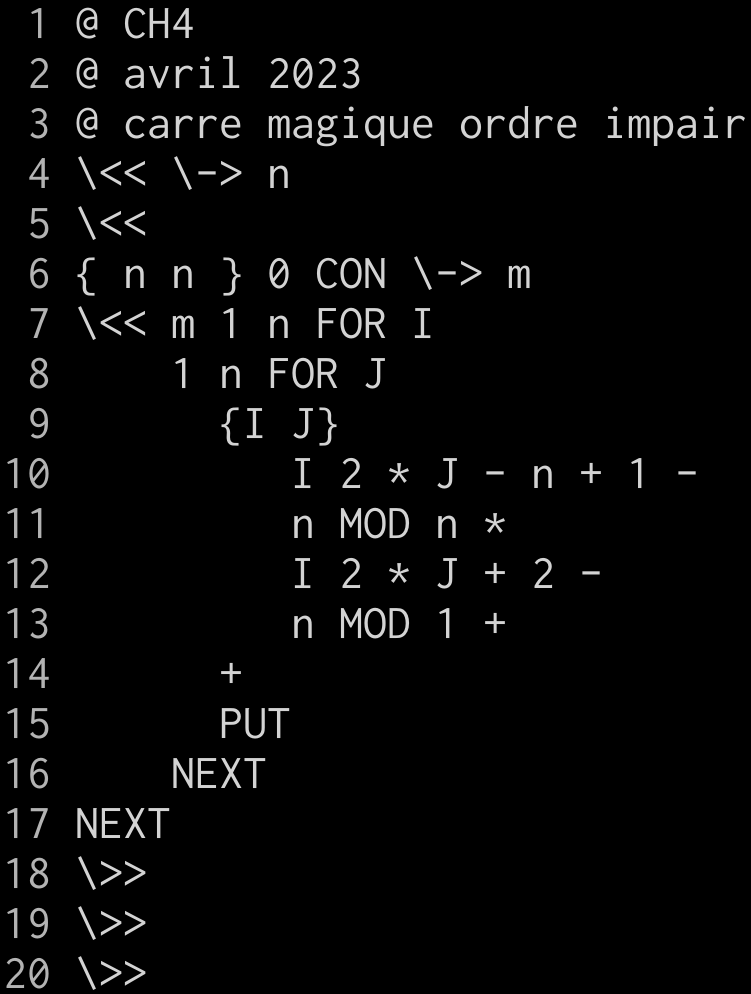
165493278

CHALLENGE #4

Voici le code t r o u v é s u r r o s e t t a c o d e .o r g que j’ai traduit :

=== HP48+ - Eric Schraf === (code IS-BASIC sur rosetta.org)

« → n
« 1 n FOR i
  1 n FOR j
  2 i * DUP j - n + 1 - n MOD n *
  SWAP j + 2 - n MOD + 1 +
  NEXT NEXT
  N DUP 2 →LIST →ARRY
» »

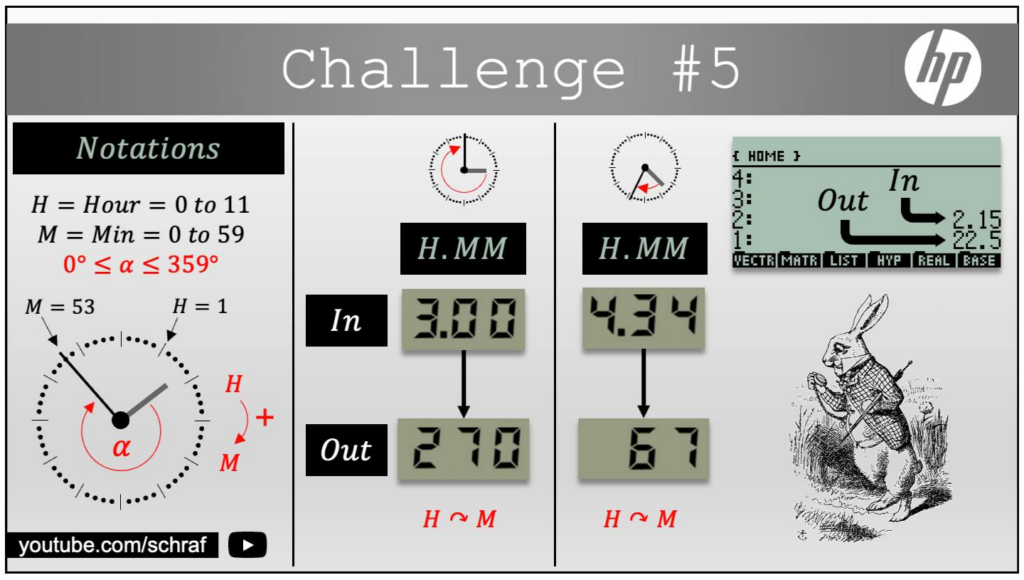
CHALLENGE #5

Chaque minute, la grande aiguille avance de 6° et la petite de 0,5° (car 30° en 60 minutes)
HH.MM correspond à 60 * HH + MM minutes. La grande aiguille sera à l’angle 360 * HH + 6 * MM et la petite aiguille en 30 * HH + 0,5 * MM. L’angle entre les 2 = 330 * HH + 5,5 * MM

=== HP48+ - Eric Schraf ===

« DUP FP 550 *
  SWAP IP 330 * + 360 MOD »

ou encore :

« DUP FP 580 *
  SWAP 30 * - 360 MOD »

=== HP 35S, 33S... - Werner Huysegoms ===

00 { 26-Byte Prgm }
01▸LBL "H.M∡"
02 ENTER
03 FP
04 580
05 ×
06 X<>Y
07 30
08 ×
09 -
10 360
11 MOD
12 END

=== Version Python - Eric Schraf ===

def ch05(hmm):
  return round((580 * (hmm % 1) - 30 * hmm) % 360, 2)

>> ch05(3.00)
270.0
>> ch05(4.34)
67.0
>> ch05(2.15)
22.5

=== Version APL n°1 - Eric Schraf ===

      ch05 ← 360 | (580 × 1 | ⊢) - 30 × ⊢

      ch05¨ 3 4.34 6 2.15
270 67 180 22.5

=== Version APL n°2 - Eric Schraf ===

      ch05 ← 360 | 580 30 -.× (1 | ⊢), ⊢

      ch05¨ 3 4.34 6 2.15
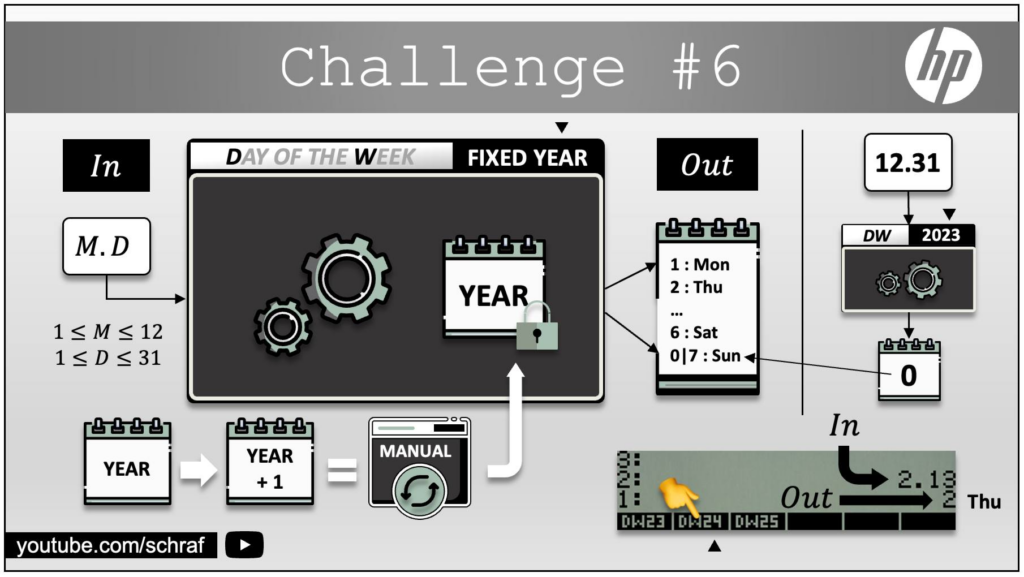
270 67 180 22.5

CHALLENGE #6

Pour les calculatrices ayant la fonction DDAYS (nombre de jours entre 2 dates), il suffisait de compter le nombre de jours entre la date voulue et un dimanche quelconque, par exemple le 2/2/3000 (date très éloignée dans le futur !). Ensuite on regarde le reste de la division de ce nombre de jours par 7.

=== HP48+ - Joseph Horn ===

« 2.023 SWAP DDAYS 7 MOD »

=== HP12C ===

01-36		ENTER
02-02		2
03-00		0
04-02		2
05-03		3		'A changer chaque année
06-26		EEX
07-06		6
08-16		CHS
09-40		+
10-02		2
11-48		.
12-00		0
13-02		2
14-03		3
15-43.26	g DYS
16-07		7
17-10		/
18-43.24	g FRAC
19-01		1
20-30		-
21-07		7
22-20		×
23-16		CHS
24-31		R/S
25-43.33.01	g GTO 01

Si maintenant votre calculatrice n’a pas la fonction DDAYS, vous pouvez utiliser la formule générale : jour_sem = jour + code(mois) + an + [an / 4] – 2 pour les années de la forme 20an. Je vous conseille ma vidéo Youtube à ce sujet.

Les codes des mois sont “144025036146”

Année 2023 (an = 23) : an + [an / 4] – 2 = 23 + [23 / 4] – 2 = 26 = 5 modulo 7.
On ajoute donc +5 aux codes des mois ce qui donne “622503514624” (toujours modulo 7).

Année 2024 (an = 24) : an + [an / 4] – 2 = 24 + [24 / 4] – 2 = 28 = 0 modulo 7.
Mais attention, 2024 est une année bissextile, plus précisément elle l’est à partir du 1er mars, avant on ne voit pas la différence avec une année “normale”. Il faut donc enlever 1 pour janvier et février, ce qui donne le code “034025036146”

=== HP48+ (Pour l'année 2023) - Eric Schraf ===

« DUP FP 2 ALOG * SWAP IP DUP
"622503514624" UNROT SUB
OBJ→ + 7 MOD »

=== HP48+ (Pour l'année 2024) - Eric Schraf ===

« DUP FP 2 ALOG * SWAP IP DUP
"034025036146" UNROT SUB
OBJ→ + 7 MOD »

=== HP 33S, 35S... - Eric Schraf ===

00001  ENTER
00002  FP
00003  100
00004  ×
00005  x<>y
00006  IP
00007  +/-
00008  10^x
00009  426415305226   (pour 2023)
00010  ×
00011  FP
00012  10
00013  ×
00014  IP
00015  +
00016  7
00017  RMDR

=== APL - Eric Schraf ===

      ch06 ← {7 | (100 × 1|⍵) + ⍎ '622503514624'[⌊⍵]}

      ch06¨ 12.31 4.04 10.27
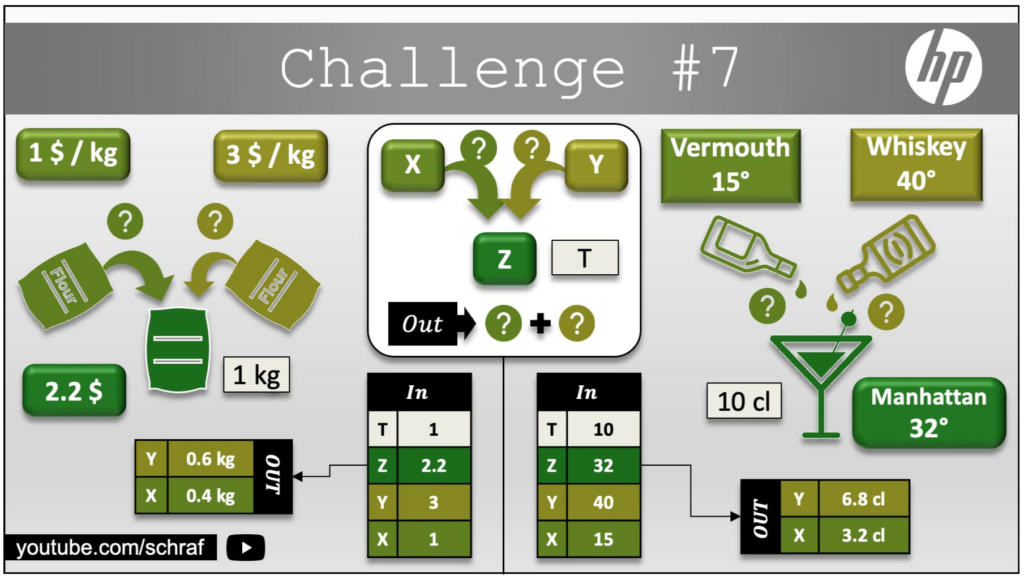
0 2 5

CHALLENGE #7

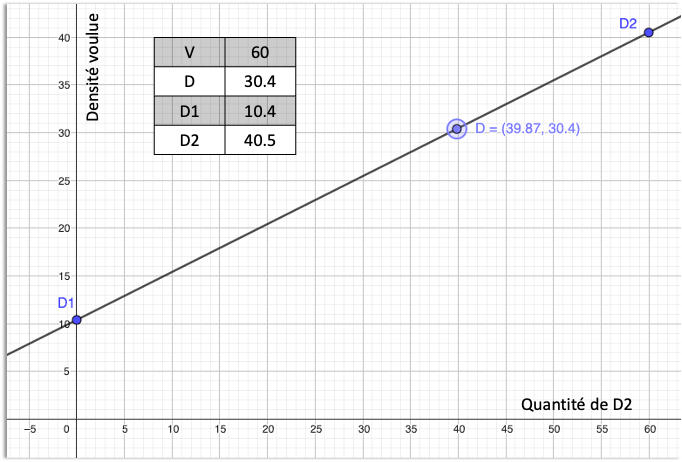
V	60
D	30.4
D1	10.4
D2	40.5

Exemple de données initiales : On veut 60L d’un liquide à 30,4°C en mélangeant des liquides à 10,4°C et 40,5°C.

Formules permettant de déterminer les volumes respectifs à utiliser.

=== HP 42S, 41C... - Werner Huysegoms ===

00 { 16-Byte Prgm }
01▸LBL "IPOL"
02 STO- ST Z
03 -
04 ÷
05 ×
06 STO- ST Y
07 X<>Y
08 END

=== HP Prime - Uwe Sauerland ===

EXPORT ch07(p1, p2, p3, m)
BEGIN
  LOCAL m1 := (p3 - p2) / (p1 - p2);
  RETURN m * { m1, 1 - m1 };
END;

=== HP 33S, 35S - Eric Schraf ===

Pas     Code (42 octets)
00001   FN = F
00002   SOLVE X
00003   V-X
00004   STOP
F0001   LBL F
F0002   SF 11
F0003   V×(D-B)÷(A-B)=X
F0004   RTN

=== Autre version pour HP 33S, 35S - Eric Schraf ===
'On cherche l'équation de la droite passant par (0, D1) et (V, D2)
'puis l'abscisse qui donnera D en ordonnée
'Visuel ci-dessous

Pas     Code (36 o)
00001   CLΣ
00002   R↑
00003   Σ+
00004   LASTx
00005   R↓
00006   CLx
00007   Σ+
00008   R↓
00009   R↓
00010   x̂
00011   -
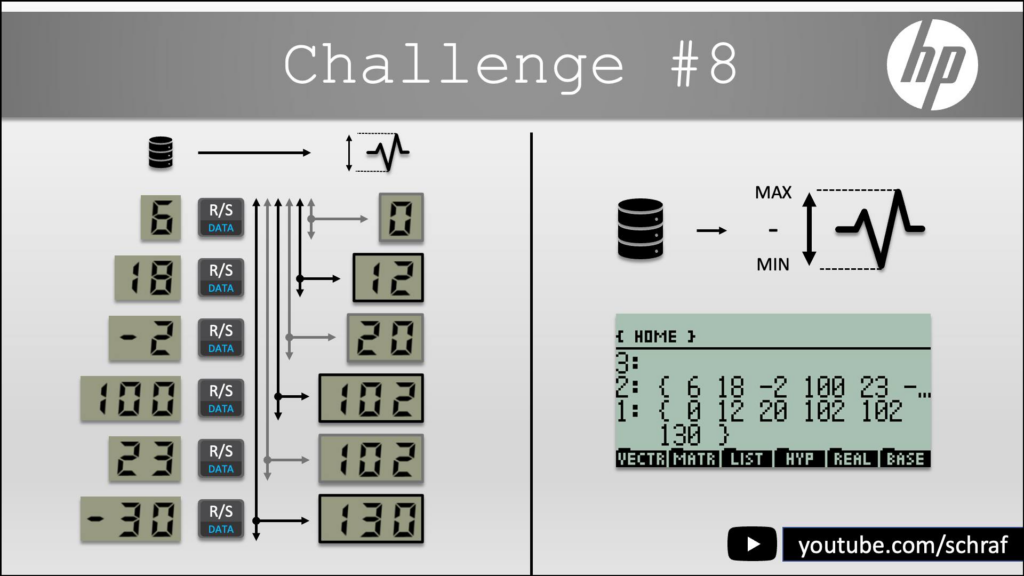
00012   LASTx

Challenge #8

=== HP 41C + compatible - Werner Huysegoms ===

GTO "CH8", then 6 R/S 18 R/S etc

00 { 23-Byte Prgm }
01▸LBL "CH8"
02 0
03▸LBL 10      @ M-m m
04 STOP        @ X M-m m
05 RCL ST Z
06 -           @ X-m M-m m
07 X>Y?
08 X<>Y
09 X>0?
10 CLX
11 STO+ ST Z
12 -
13 GTO 10
14 END

=== HP48g+ - Werner Huysegoms ===

CH8: « DUP LMAX SWAP LMIN - »
LMAX: « 0 « OVER MAX » FLIST »
LMIN: « DUP HEAD « OVER MIN » FLIST »
FLIST: « ROT 1 ROT DOSUBS SWAP DROP »

=== HP48g+ - Eric Schraf ===

SCA: « → v f « v « OVER f EVAL » STREAM v SIZE →LIST »
CH8: « DUP « MAX » SCA SWAP « MIN » SCA - »

=== APL - Eric Schraf ===

      ch08 ← ⌈\ - ⌊\

      ch08 6 18 ¯2 100 23 ¯30
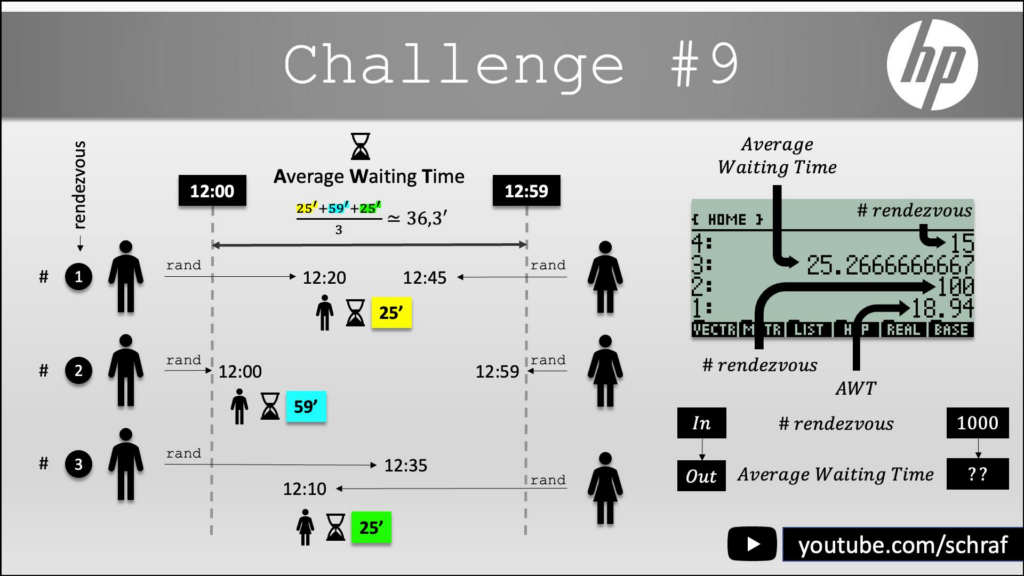
0 12 20 102 102 130

Challenge #9

Le calcul mathématique du temps d’attente du premier arrivé au rendez-vous n’est pas simple ! Par contre, par simulation, on obtient facilement une estimation du résultat. En effet, il suffit pour chaque expérience de tirer 2 nombres entiers entre 0 et 59 et de regarder leur différence en valeur absolue (qui est donc le temps d’attente du premier arrivé). On recommence l’expérience des centaines ou milliers de fois et on constate qu’en moyenne le temps sera de 20 minutes.

=== HP 42S - Werner Huysegoms ===

00 { 43-Byte Prgm }
01▸LBL "CH09"
02 STO "N"
03 STO "M"
04 0
05▸LBL 10
06 XEQ 14
07 XEQ 14
08 -
09 ABS
10 +
11 DSE "M"
12 GTO 10
13 RCL÷ "N"
14 RTN
15▸LBL 14
16 RAN
17 60
18 ×
19 IP
20 END

=== HP 48+ - Werner Huysegoms ===

« → N «
0 1 N START
R59 R59 - ABS + NEXT
N / » »

'R59':
« RAND 60 * IP »

=== HP Prime - Uwe Sauerland ===

EXPORT ch09(samples)
BEGIN
 LOCAL k, totalWT := 0;
 FOR k FROM 1 TO samples DO
  LOCAL sample := ABS(deltalist(RANDINT(2, 0, 59)));
  totalWT := totalWT + sample(1);
 END;
 return totalWT / samples;
END;

=== Version APL ===

      ch09 ← { ⍵ ÷⍨ +/ | - ⌿ ? 2 ⍵ ⍴60 }

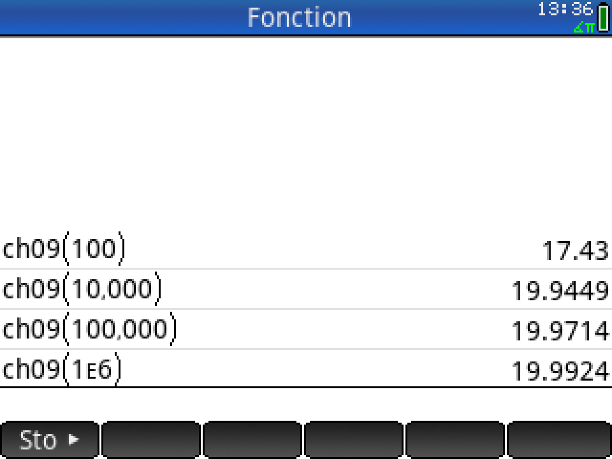
      ch09 100
18.94
      ch09 10000
20.0471
      ch09 100000
20.04593
      ch09 1000000
19.996039