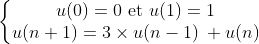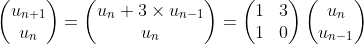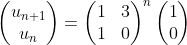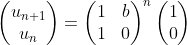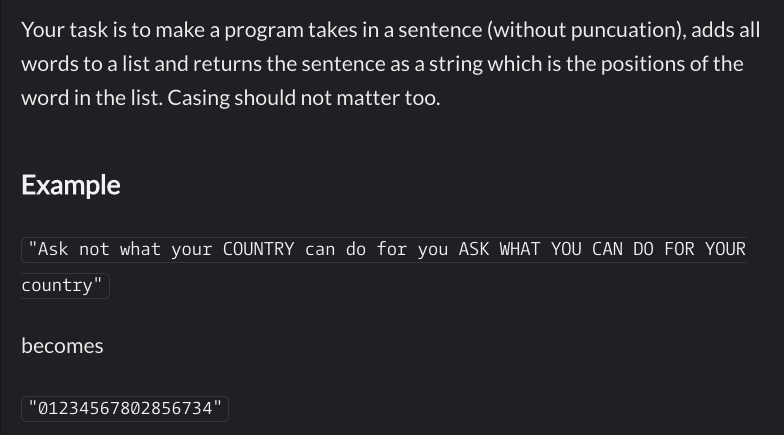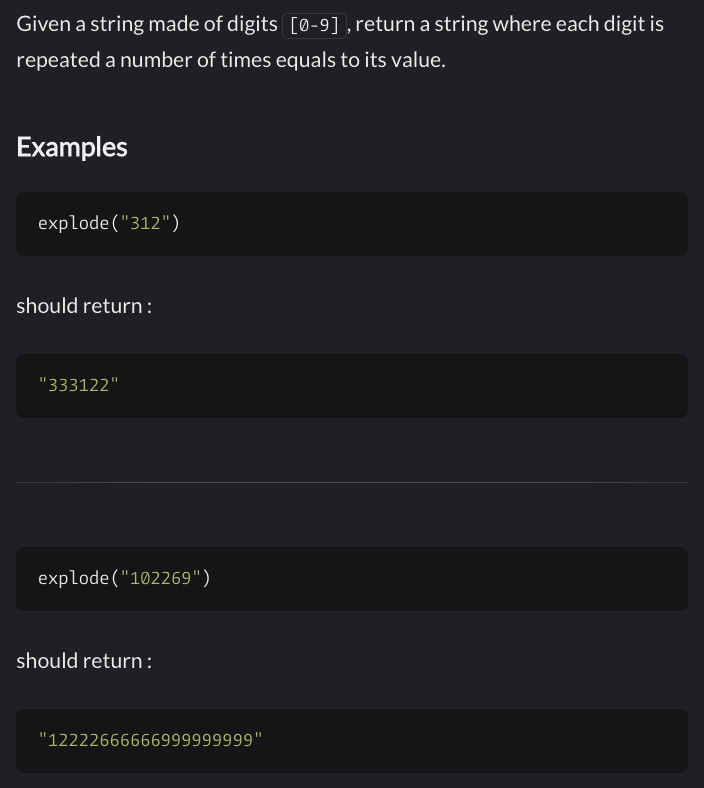
Résumé en français : On vous donne une liste contenant des couleurs de moufles (donc pas de main gauche ou droite à distinguer). On vous demande le nombre de paires que vous pouvez constituer, c’est-à-dire avoir 2 moufles de la même couleur.
Avec le premier exemple donné, on peut constituer une paire de moufles rouge (red) et une paire bleue (blue) soit 2 paires.
Version classique
Relisez l’exercice 6 que j’ai proposé, vous devriez constater de nombreuses ressemblances.
Une première idée est de commencer par récupérer les différentes couleurs puis, pour chacune d’elle, de compter combien de fois cette couleur apparait. Il suffira de diviser par 2 ce nombre (sans tenir compte des virgules) pour savoir combien de paires on peut constituer avec cette couleur. Finalement, on fera la somme du nombre de paires trouvées.
python
Je reprends la structure classique vue dans l’exercice 6 :
def nb_paires(gants):
couleurs = [ ] # couleurs distinctes
for g in gants: # on parcourt les gants
if g not in couleurs: # nouvelle couleur ?
couleurs.append(g) # on l'ajoute à la liste
paires = 0 # nombre de paires possibles
for c in couleurs: # on parcourt à nouveau les gants
paires += gants.count(c) // 2 # on compte puis ÷ entière par 2
return paires # on renvoie le nombre de paires
>> nb_paires(["gray","black","purple","purple","gray","black"])
3
>> nb_paires(["red","green","blue"])
0javascript
A nouveau je reprends la structure de l’exercice 6 :
const nb_paires = gants =>
{
couleurs = gants.reduce((a, g) =>
a.includes(g) ? a : a.concat(g), []);
paires = 0;
for (c of couleurs)
{
paires += Math.floor(gants.filter(g => g == c).length / 2)
}
return paires
}
>> nb_paires(["gray","black","purple","purple","gray","black"])
3
>> nb_paires(["red","green","blue"])
0Remarque : La division entière par 2 ou des puissances de 2 (c’est-à-dire 4, 8, 16, 32…) peut se faire autrement. En effet, si un nombre est écrit en binaire, diviser par 2 revient à supprimer l’unité (bit le plus à droite) :
>> (13).toString(2) // 13 en binaire. Python : bin(13) → '0b1101'
'1101'
>> (6).toString(2) // Diviser par 2 = supprimer l'unité
'110'La raison est que 13 = 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 = 11012. En divisant par 2, toutes les puissances vont diminuer de 1 : 6 = 1 * 2^2 + 1 * 2^1 + 0 * 2^0 = 1102
On utilise >> pour décaler un bit vers la droite en Python et JavaScript :
13 >> 1
6De la même façon, on peut diviser par 4, multiplier par 8 etc :
13 >> 2 // Diviser par 4 (c'est-à-dire ÷ 2 fois par 2)
3
13 << 3 // Multiplier par 8 (c'est-à-dire × 3 fois par 2)
104Version ensembliste
Comme nous l’avons également vu dans l’exercice 6, nous pouvons utiliser des ensembles (set) pour récupérer les éléments uniques. Les versions sont alors nettement plus courtes :
Python
def nb_paires(gants):
return sum(gants.count(v) // 2 for v in set(gants))
JavaScript
const nb_paires = gants => [...new Set(gants)]
.reduce((a,v) => a + (gants.filter(c => c == v).length >> 1), 0)apl
Toujours dans l’exercice 6, nous avons vu l’utilisation de ⌸ (key), qui permet de synthétiser des informations. Ici, nous voulons pour chaque couleur distincte, compter combien de fois elle apparait dans la liste et diviser cette valeur par 2 (sans virgule). Ecrivons cela étape par étape :
gants ← 'gray' 'red' 'purple' 'purple' 'gray' 'black'
{⍺, ⍵}⌸ gants ⍝ Positions des couleurs dans le vecteur
┌──────┬─┬─────┐
│gray │1│5 │
├──────┼─┼─────┤
│red │2│ │
├──────┼─┼─────┤
│purple│3│4 │
├──────┼─┼─────┤
│black │6│ │
└──────┴─┴─────┘
{⍺, ⍴⍵}⌸ gants ⍝ Nombre d'apparitions de chaque couleur
┌──────┬─┐
│gray │2│
├──────┼─┤
│red │1│
├──────┼─┤
│purple│2│
├──────┼─┤
│black │1│
└──────┴─┘
{⍴⍵}⌸ gants ⍝ Uniquement le nombre d'apparitions
2
1
2
1
{.5 × ⍴⍵}⌸ gants ⍝ Division par 2
1
0.5
1
0.5
{⌊ .5 × ⍴⍵}⌸ gants ⍝ avec partie entière
1
0
1
0
+⌿ {⌊ .5 × ⍴⍵}⌸ gants ⍝ Somme de la colonne
2Le programme final APL à tester ici :
nb_paires ← +⌿ {⌊ .5 × ⍴⍵}⌸
nb_paires 'red' 'green' 'red' 'blue' 'blue'
2
nb_paires 'red' 'green' 'blue'
0Python et JavaScript : Version utilisant une seule boucle et une pile
Est-il vraiment nécessaire de récupérer les couleurs uniques ? Imaginons la situation dans la vie réelle avec ‘red’ ‘green’ ‘red’ ‘blue’ ‘blue’ :
- Dans ma tête je pense à 0, c’est le nombre de paires que j’ai réussi à faire
- Je prends le premier gant, il est ‘red’, je n’ai pas cette couleur donc je la garde
- Je prends le deuxième, il est ‘green’, je n’ai pas cette couleur donc je la garde
- Je prends le troisième, il est ‘red’. J’ai déjà cette couleur, je peux donc faire une paire. J’enlève les 2 moufles ‘red’ et j’ajoute 1 au nombre de paires
- Je prends le quatrième, il est ‘blue’, je n’ai pas cette couleur donc je la garde
- Je prends le cinquième, il est ‘blue’. J’ai déjà cette couleur, je peux donc faire une paire. J’enlève les 2 moufles ‘blue’ et j’ajoute 1 au nombre de paires
- J’ai finalement réussi à constituer 2 paires.
🤖 Refaites de tête le processus avec les gants ‘red’ ‘red’ ‘red’ ‘red’ ‘red’
Prendre un gant revient à ajouter un élément dans une liste, inversement créer une paire à éliminer cette couleur de la liste. Voyons comment ajouter, enlever ou tester si un élément est dans un ensemble en utilisant les méthodes add, remove, delete :
python
>> paires = set() # Ensemble vide
>> paires.add('red') # on ajoute 'red' à l'ensemble
>> paires
{'red'}
>> paires.add('blue')
>> paires
{'red', 'blue'}
>> paires.remove('red') # on enlève 'red'
>> paires
{'blue'}
>> 'red' in paires # on teste si 'red' est dans l'ensemble
Falsejavascript
>> paires = new Set() // Ensemble vide
>> paires.add('red') // on ajoute 'red' à l'ensemble
Set(1) {'red'}
>> paires.add('blue')
Set(2) {'red', 'blue'}
>> paires.delete('red') // on enlève 'red'
>> paires
Set(1) {'blue'}
>> paires.has('red') // on teste si 'red' est dans l'ensemble
falseVersions finales basées sur cette idée :
Python
def nb_paires(gants):
couleurs = set() # les couleurs trouvées
paires = 0 # nb de paires réalisées
for c in gants: # on parcourt les gants
if c in couleurs: # couleur déjà vue ?
couleurs.remove(c) # on la retire des couleurs trouvées
paires += 1 # le nombre de paires augmente de 1
else: # sinon
couleurs.add(c) # ajouter cette nouvelle couleur
return paires # nombre de paires trouvées
JavaScript
const nb_paires = gants => {
couleurs = new Set();
paires = 0;
for (c of gants)
{
if (couleurs.has(c))
{
couleurs.delete(c);
paires ++
}
else
couleurs.add(c)
}
return paires
} 🤯 Pour terminer, voici une version (difficile à lire) avec reduce du programme JavaScript précédent :
const nb_paires = gants =>
gants.reduce((a, c) => // On parcourt les couleurs
a[1].has(c) ? // Couleur déjà vue ?
[a[0] + a[1].delete(c), a[1]] : // +1 paire et suppr couleur
[a[0], a[1].add(c)] // sinon on ajoute couleur
,[0, new Set()]) // Initialisation paires = 0 et couleurs
[0] // On récupère le nombre de pairesOn utilise le fait que true + nombre donne le même résultat que 1 + nombre :
>> a = new Set() // Ensemble vide
>> a.add('red') // on ajoute 'red'
Set(1) {'red'}
>> 3 + a.delete('red') // a.delete renvoie true qui correspond à 1
4 // Cela donne bien 3 + 1 = 4Autre version en APL
Nous avons vu le produit interne à plusieurs reprises dans les exercices. Il existe également un produit externe (noté ∘), l’exemple classique étant la table de multiplication :
(⍳5) ∘.× ⍳3 ⍝ Multiplier chaque élément de 1 2 3 4 5
1 2 3 ⍝ par chaque élément de 1 2 3
2 4 6
3 6 9 ⍝ d'où une matrice 5 x 3
4 8 12
5 10 15Voici un autre exemple :
gants ← 'red' 'green' 'red' 'blue' 'blue'
∪ gants ⍝ Eléments uniques dans le vecteur
┌───┬─────┬────┐
│red│green│blue│
└───┴─────┴────┘
gants ∘.≡ ∪ gants ⍝ On teste toutes les égalités
1 0 0 ⍝ 'red' est égal au 1er élément de ∪ gants
0 1 0 ⍝ 'vert' égal au 2e élément de ∪ gants
1 0 0 ⍝ 'red' est égal au 1er élément de ∪ gants
0 0 1 ⍝ 'blue' est égal au 32 élément de ∪ gants
0 0 1 ⍝ 'blue' est égal au 32 élément de ∪ gantsOn peut alors faire la somme des colonnes, diviser les totaux par 2 et prendre la partie entière :
⌊ .5 × +⌿ gants ∘.≡ ∪ gants
1 0 1Et finalement réduire par la somme :
+/ ⌊ .5 × +⌿ gants ∘.≡ ∪ gants
2
⍝ En faisant les produits puis la somme (produit interne +.×)
+/ ⌊ .5 +.× gants ∘.≡ ∪ gants
2
Ce qui donne cette autre version finale en APL à tester ici :
nb_paires ← {+/ ⌊ .5 +.× ⍵ ∘.≡ ∪⍵}
nb_paires gants
2🧐 Les plus attentifs d’entre vous auront remarqué que ⍵ ∘.≡ ∪⍵ peut s’écrire ⊢∘.≡∪ (fork). En effet, on applique l’union à ⍵, l’identité à ⍵ puis le test d’égalité aux 2 résultats. Or (f⍵)g(h⍵) peut s’écrire sous la forme (fgh)⍵ :
(⊢∘.≡∪) 'red' 'green' 'red' 'blue' 'blue'
1 0 0
0 1 0
1 0 0
0 0 1
0 0 1🥵 Ce qui nous amène à cette troisième version à tester ici :
nb_paires ← +/∘⌊ .5 +.× ⊢∘.≡∪
nb_paires 'red' 'green' 'red' 'blue' 'blue'
2
nb_paires 'red' 'green' 'blue'
0
