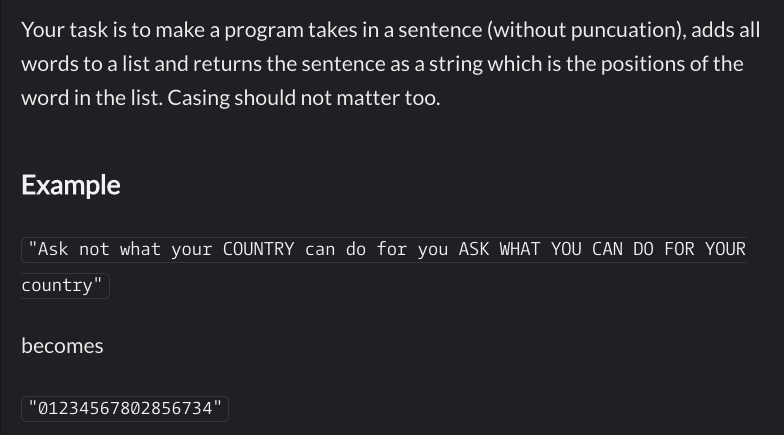
Résumé en français : Vous devez créer un programme qui à partir d’une phrase, met tous les mots distincts dans une liste et retourne une chaine donnant les positions des mots de la phrase initiale dans cette liste. On ne tiendra pas compte de la casse.
Voici un autre exemple pour mieux comprendre :
phrase = 'The number 0 is such a strange number Strangely it has zero meaning'
>> compress(phrase)
'012345617891011'En effet, la liste des mots uniques est :
['the', 'number', '0', 'is', 'such', 'a', 'strange', 'strangely', 'it', 'has', 'zero', 'meaning']Il faut donc bien voir que le mot ‘strangely’ est à la 8e place dans la phrase initiale mais à la 7e place dans la liste des mots uniques, c’est donc 7 qu’il faut récupérer en non 8.
Version classique avec boucles
On peut commencer par créer la liste des mots uniques trouvés dans la phrase et dans un second temps parcourir à nouveau tous les mots de la phrase pour trouver leurs positions dans cette liste. Première étape :
python
def compress(phrase):
mots = [] # Tableau des mots uniques
for m in phrase.lower().split(): # On parcourt chaque mot
if m not in mots: # Nouveau mot ?
mots.append(m) # On l'ajoute à la liste
return mots
>> compress('The number 0 is such a strange number Strangely it has zero meaning')
['the', 'number', '0', 'is', 'such', 'a', 'strange', 'strangely', 'it', 'has', 'zero', 'meaning']Remarquez qu’en Python, split peut s’utiliser sans paramètre (par défaut ce sera espace) :
>> 'ab cd'.split()
['ab', 'cd']On peut maintenant chercher les positions des mots dans la liste des mots uniques en utilisant index :
>> ['the', 'number', '0', 'is'].index('is') # Position de 'is' ?
3Ce qui donne cette version finale à tester ici :
def compress(phrase):
decoup = phrase.lower().split()
mots = []
for m in decoup:
if m not in mots:
mots.append(m)
return ''.join([ str(mots.index(m)) for m in decoup ])
>> compress('The number 0 is such a strange number Strangely it has zero meaning')
'012345617891011'str permet de convertir un nombre en chaine.
javascript
La première partie pour rechercher les mots uniques peut être faite comme en Python ou en utilisant reduce (puisque l’on part d’un tableau vide [ ] et que l’on va ajouter au fur et à mesure les mots nouveaux). Ce qui donne :
var compress = phrase => {
decoup = phrase.toLowerCase().split(' ')
mots = decoup.reduce((a, m) => a.includes(m) ? a : a.concat(m), [])
return mots
}
>> compress('The number 0 is such a strange number Strangely it has zero meaning')
['the', 'number', '0', 'is', 'such', 'a', 'strange', 'strangely', 'it', 'has', 'zero', 'meaning']Ensuite, pour la seconde partie, il s’agit de transformer (map) chaque mot en sa position dans la liste des mots uniques. Voici 2 exemples d’utilisation de map :
>> [1, 5, 10].map(v => v * v) // On met chaque élément au carré
[1, 25, 100]
>> ['abra','cada','bra'].map(m => m[0].toUpperCase())
['A', 'C', 'B'] // Première lettre de chaque mot en majusculeD’où cette version finale à tester ici :
var compress = phrase => {
decoup = phrase.toLowerCase().split(' ')
mots = decoup.reduce((a, m) => a.includes(m) ? a : a.concat(m), [])
return decoup.map(m => '' + mots.indexOf(m)).join('')
}Le » + permet de convertir un nombre en chaine. Par exemple » + 2 donne ‘2’, on peut aussi utiliser (2).toString().
Autres pistes : dictionnaires, ensembles…
Nous avons déjà vu l’utilisation de set pour créer des ensembles en Python/JavaScript et APL (∪). La première partie peut alors se simplifier en :
javascript
var compress = phrase => {
decoup = phrase.toLowerCase().split(' ')
mots = [...new Set(decoup)] // Liste des mots uniques
return decoup.map(m => '' + mots.indexOf(m)).join('')
}
>> compress('The number 0 is such a strange number Strangely it has zero meaning')
'012345617891011'python
Nous aurions également pu utiliser un dictionnaire, voici une écriture en Python :
>> dict.fromkeys('a b B A C b a'.lower().split())
{'a': None, 'b': None, 'c': None}
>> list(dict.fromkeys('a b B A C b a'.lower().split()))
['a', 'b', 'c']Ce qui donne ce programme final :
def compress(phrase):
decoup = phrase.lower().split()
mots = list(dict.fromkeys(decoup)) # Liste des mots uniques
return ''.join(str(mots.index(m)) for m in decoup)APL
Nous avons déjà vu dans l’exercice précédent comment séparer les mots en utilisant ⊆ :
{(' '≠⍵) ⊆ ⎕C ⍵} 'LisTe dE MotS'
┌─────┬──┬────┐
│liste│de│mots│
└─────┴──┴────┘Et ⍳ (iota) permet (en version dyadique, c’est-à-dire avec 2 arguments) de trouver la position d’une valeur dans un vecteur :
4 8 7 9 ⍳ 7 ⍝ Quelle est la position du 7 dans le vecteur ?
3Pour récupérer les mots uniques, on peut utiliser ∪ ou key (⌸) plus général qui permet de synthétiser des informations :
{⍺,⍵}⌸ 'a' 'b' 'b' 'a' 'c' 'b' 'a' ⍝ Lettres et positions
a 1 4 7
b 2 3 6
c 5
{⍺}⌸ 'a' 'b' 'b' 'a' 'c' 'b' 'a' ⍝ Que les lettres
abc
∪ 'a' 'b' 'b' 'a' 'c' 'b' 'a' ⍝ Plus simple avec ∪
abcUn exemple pour mieux comprendre l’utilisation de ⍳ :
'un' 'deux' 'trois' ⍳ 'deux' 'deux' 'trois' 'un' 'un'
2 2 3 1 1Ce qui signifie : quelles sont les positions des mots ‘deux’ ‘deux’ ‘trois’ ‘un’ ‘un’ dans le vecteur ‘un’ ‘deux’ ‘trois’ ?
Enfin, en APL, il est possible de simplifier des écritures du type :
(⍺ f ⍵) g (⍺ h ⍵)C’est-à-dire calculer ⍺ f ⍵ où f est une fonction dyadique, calculer ⍺ h ⍵ avec h également dyadique et enfin appliquer g aux 2 résultats trouvés (g dyadique également). La version simplifiée est :
⍺ (f g h) ⍵Exemple avec f = +, h = ⌈ et g = × :
(2 + 3) × (2 ⌈ 3) ⍝ 5 × 3 (= le plus grand entre 2 et 3)
15
2 (+ × ⌈) 3 ⍝ Notation appelée "train" ou "fork"
15De la même façon :
(f ⍵) g (h ⍵) peut s'écrire (f g h) ⍵Exemple :
(⌊/ × ⌈/) 3 7 2 9 5
18Explications : On cherche la plus petite des valeurs (⌊/), c’est-à-dire 2 et la plus grande (⌈/) c’est-à-dire 9 puis on les multiplie, ce qui donne 18.
Programme final en APL :
⎕IO ← 0
compress ← {,/⍕¨(∪ ⍳ ⊢)(' '≠⍵) ⊆ ⎕C ⍵}
compress 'The number 0 is such a strange number Strangely it has zero meaning'
┌───────────────┐
│012345617891011│
└───────────────┘
Le ,/ sert à concaténer les termes et ⍕¨ à convertir en chaine chaque position numérique trouvée.
La traduction du programme est donc : Prendre le paramètre (⍵), le convertir en minuscules (⎕C), séparer la phrase en utilisant les espaces (‘ ‘≠⍵) ⊆, prendre les éléments uniques (∪) et cherchez les positions (⍳) des mots (⊢ correspond à ce que l’on a à droite). Transformez toutes les positions en chaines (⍕¨) et en faire la concaténation (,/).