En APL il existe l’opérateur \ (appelé scan ou balayage ou réduction partielle) qui fait penser à l’opérateur / de réduction. Voici la différence :
f/ 1 2 3 … = 1 f 2 f 3 … f\ 1 2 3 … = (f/1) (f/1 2) (f/1 2 3) …
Le n-ieme résultat est égal à la réduction des n premiers éléments. L’exemple de base est la somme cumulée des éléments d’un vecteur :
+\ 2 3 4 8 10 2 5 9 17 27
On peut imaginer une version en RPL utilisant SEQ pour créer ces suites ou rester avec notre trio DOLIST, DOSUBS et STREAM. En effet, si on reprend la réduction :
1: { 2 3 4 8 10 }
« + »
PRG LIST PROC STREAM
1: 27
Mais si l’on ajoute OVER pour dupliquer à chaque fois le résultat précédent :
1: { 2 3 4 8 10 }
« OVER + »
PRG LIST PROC STREAM
5: 2
4: 5
3: 9
2: 17
1: 27
On obtient les bonnes valeurs mais elles seront sur la pile. Pour comprendre le principe, tapez sur votre machine :
2 ENTER 3 OVER + 4 OVER + 8 OVER + 10 OVER +
Reste à la transformer en liste { 2 5 9 17 27}. On peut imaginer cette version pour le cas d’une somme cumulée :
« → v
« v « OVER + » STREAM v SIZE →LIST »
»
'SCUM STO
1: { 2 5 3 4}
VAR SCUM
1: {2 7 10 14}
Ou, de façon plus générale, définir SCA. (Scan), appelé PRED dans le document d’origine de Norman Brenner) :
« → v f « v « OVER f EVAL » STREAM v SIZE →LIST » » 'SCA. STO
Exemples :
1: {1 2 3 4}
2: « + »
VAR SCA.
1: {1 3 6 10}
1: {2 5 4 1 8 3 3}
2: « MAX »
VAR SCA.
1: {2 5 5 5 8 8 8} # Maximum progressif
En APL :
⌈\ 2 5 4 1 8 3 3
2 5 5 5 8 8 8
En particulier, lorsque les vecteurs sont binaires, cela permet d’avoir des résultats intéressants :
∧\ 1 1 1 0 1 0 0 1 1 1 1 0 0 0 0 0 ⍝ = 0 à partir du 1er "0" ∨\ 0 0 0 0 1 0 0 1 0 0 0 0 1 1 1 1 ⍝ = 1 à partir du 1er "1" <\ 0 0 1 0 1 1 0 0 1 0 0 1 0 0 0 0 0 0 ⍝ Position du 1er "1"
En RPL :
2: {1 1 1 0 1 0 0 1}
1: « AND »
VAR SCA.
1: {1 1 1 0 0 0 0 0}
2: {0 0 0 0 1 0 0 1}
1: « OR »
VAR SCA.
1: {0 0 0 0 1 1 1 1}
Lorsque l’opérateur f est commutatif (comme OR, AND, +, MAX…) il n’y a pas de différence entre le RPL et l’APL. Par contre, pour des opérateurs non commutatifs comme « <« , le résultat sera faux.
APL : f\ a b c = (a) (a f b) (a f (b f c))
RPL : f\ a b c = (a) (a f b) ((a f b) f c)
Pour se convaincre :
2: {0 0 1 0 1 1 0 0 1}
1: « < »
VAR SCA.
1: {0 0 0 0 0 0 0 0 0}
Résultat attendu : 0 0 1 0 0 0 0 0 0
Exercice – Les immeubles
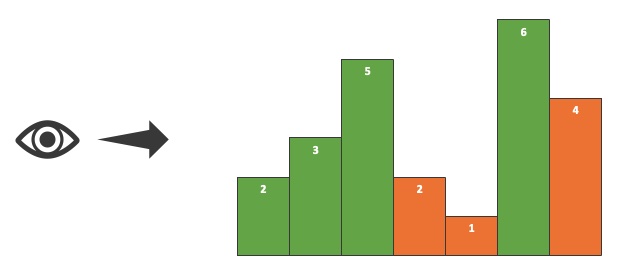
On vous donne une liste de hauteurs d’immeubles adjacents et on vous demande combien seront visibles si vous les regardez à partir de la gauche. Par exemple, si les hauteurs sont 2 3 5 2 1 6 4, en vert ci-dessous les 4 seuls immeubles qui seront visibles (les autres sont cachés par des bâtiments plus hauts)
On supposera dans un premier temps qu’il n’y a pas de zones vides entre les immeubles, c’est-à-dire que la liste ne contient pas de 0 (immeubles de hauteur nulle).
IMM 2 3 5 2 1 6 4 Output: 4
Dans un second temps, considérez le cas général.
Corrigé version 1 : Commençons par l’APL. On va déjà scanner les immeubles pour récupérer les hauteurs maximales atteintes :
⌈\ 2 3 5 2 1 6 4 Output: 2 3 5 5 5 6 6
Il faut maintenant récupérer les hauteurs distinctes :
∪ ⌈\ 2 3 5 2 1 6 4 Output: 2 3 5 6
Et les compter :
⍴ ∪ ⌈\ 2 3 5 2 1 6 4 Output: 4
Le programme final en APL pour la version 1 :
IMM ← {⍴∪⌈\⍵}
Nous pouvons immédiatement traduire cela en RPL avec les programmes SCA. (scan), UN. (union) et la fonction SIZE :
« « MAX » SCA. UN. SIZE » 'IMM STO
Vérifions :
1: { 2 3 5 2 1 6 4 }
VAR IMM
1: 4.
Corrigé de la version générale : Si la liste commence par un ou plusieurs 0, le calcul sera faux :
1: { 0 2 1 }
VAR IMM
1: 2.
Ceci parce que les maximums progressifs sont { 0 2 2 } dont la réunion comporte 2 termes {0 2}. Il faut donc filtrer la liste des maximums pour enlever les 0. Une solution possible en APL :
IMM ← {⍴∪ (0 ≠ n) / n ← ⌈\⍵}
Et nous avions créer en RPL la fonction CL. pour compresser une liste en utilisant un vecteur logique. D’où cette version en RPL :
« « MAX » SCA. DUP 0 > CL. UN. SIZE » 'IMM STO
Qui signifie prendre les maximums progressifs, dupliquer cette liste, créer le vecteur logique des termes > 0, éliminer les éléments qui sont à FAUX, faire la réunion des éléments restants et les compter.
1: { 0 2 1 }
VAR IMM
1: 1.
Exemple – Les fractions continues
Pour la définition d’une fraction continue, voir par exemple Wikipedia.
En APL, on obtient la valeur approchée d’une liste d’étages par :
+∘÷/ 1 2 2 2 2 1.413793103
Qui correspond à la valeur 1 + 1 / ( 2 + 1 / ( 2 + 1 / ( 2 + 1 / 2 ) ) )
Et en utilisant un scan :
+∘÷\ 1 2 2 2 2 1 1.5 1.4 1.416666667 1.413793103
On obtient les fractions 1, puis 1 + 1 / 2 puis
1 + 1 / (2 + 1 / 2)…
En RPL, on peut obtenir la valeur finale par :
« REVLIST « OVER INV + » STREAM →NUM »
'FC STO
1: { 1 2 2 2 2 }
VAR FC
1: 1.41379310345 # ≃ racine de 2
1: { 1 1 1 1 1 1 1 1 1 1 }
VAR FC
1: 1.61818181818 # ≃ nombre d'or
L’opération « Prendre l’inverse plus additionner » n’étant pas commutative, on ne pourra pas utiliser notre fonction SCA.