Suite à un post de FLISZT publié sur le forum Silicium.org, je vous propose de reprendre quelques éléments trouvés dans le document de Norman Brenner. Il s’agit de traduire certaines des fonctions APL (sélection, réduction, transformation…) en RPL pour les calculatrices HP-48/49/50G
Machines utilisées
Création d’un répertoire APL sur les HP
HP 48G : ↱ MEMORY NEW HP 49/50 : ↰ FILES
Puis :
NAME : APL ☑ DIRECTORY OK
Ou encore en tapant la commande :
'APL' ALPHA ALPHA CRDIR
Pour se déplacer dans le répertoire {HOME APL} :
VAR APL
Pour revenir à la racine {HOME} :
HP 48G : ↱ HOME HP 49/50G : ↰ UPDIR (ENTER sur HP 49)
Par la suite, nous travaillerons dans le répertoire {HOME APL}
Exemple 1 – Compression logique
Ecrire un programme RECUS qui à partir d’une liste (vecteur en APL) de notes d’étudiants renvoie la liste des notes ≥ 10.
Résultat attendu en APL
RECUS 5 12 13 8 17 2 12 13 17
Résultat attendu en RPL
1: {5 12 13 8 17 2}
VAR RECUS
1: {12 13 17}
En APL, la compression logique est une fonction dyadique (2 arguments), celui de gauche est un vecteur logique (1 ou 0) et celui de droite un vecteur quelconque. Le résultat sera le vecteur composé uniquement des éléments associés aux 1. Exemple :
1 0 1 / 5 12 13 5 13 ⍝ On garde 1er et 3e éléments
Vous pouvez tester la commande en direct ici.
Voici la traduction proposée par Norman Brenner pour la Compression Logique que nous noterons CL. (BSEL dans le document initial) :
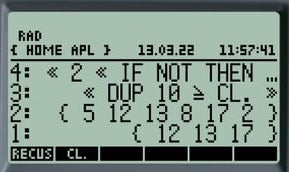
« 2 « IF NOT THEN DROP END » DOLIST » 'CL. STO # On mémorise le programme
Avant les explications et une simplification, voyons son utilisation :
2: {5 12 13 8 17 2} # Notes au niveau 2
1: {0 1 1 0 1 0} # Masque booléen niveau 1
VAR CL. # On lance le programme
1: {12. 13. 17.} # Résultat au niveau 1
DOLIST permet d’appliquer une fonction ou un programme à un groupe de listes. Il faut pour cela saisir des listes, le nombre de listes à traiter et le programme ou la fonction à exécuter.
Le programme CL. indique qu’il y a 2 listes à traiter. Il prend ensuite la négation de la liste du niveau 1 (Ainsi les 0 deviennent des 1 et réciproquement) et applique DROP pour éliminer les éléments correspondant à 1. Voici 2 exemples illustrant l’utilisation de NOT et DOLIST :
{0 1 1 0 1 0} # Liste de booléens
ALPHA ALPHA NOT
{1 0 0 1 0 1} # Négation
4: {5 3 1 4} # Les listes à traiter
3: {7 2 8 2}
2: 2 # Nb de listes
1: « MAX » # Fonction à appliquer
PRG LIST PROC DOLIST
1: {7. 3. 8. 4.} # Max entre les 2 listes
Nous pouvons maintenant créer notre programme RECUS, pour cela il faut fournir à CL. la liste des notes ainsi qu’un “vecteur” logique précisant lesquelles sont ≥ 10. Pour cela on duplique la liste et on effectue le test 10 ≥ :
« DUP 10 ≥ CL.» 'RECUS STO # On mémorise le programme
Les 2 programmes CL. et RECUS et application de RECUS à la liste {5 12 13 8 17 2}
En APL, le programme pourrait être :
RECUS ← {(⍵ ≥ 10) / ⍵}
RECUS 5 12 13 8 17 2
Output : 12 13 17
On peut également utiliser IFT pour sélectionner les éléments d’une liste et enlever les autres, en effet :
1: {0 1 1 0 1 0}
2: {5 12 13 8 17 2}
PRG BRCH NXT IFT
1: {12 13 17}
Ainsi notre programme RECUS peut s’écrire plus simplement :
« DUP 10 ≥ SWAP IFT » 'RECUS STO
On duplique la liste (DUP), on crée le vecteur logique (10 ≥ ), on met le vecteur logique au niveau 2 (SWAP) et on applique IFT.
Ceci donne l’idée de simplifier le code CL. proposé par Norman Brenner par :
« SWAP IFT » 'CL. STO
Remarquons que l’on peut enchainer les compressions, par exemple sélectionnons les notes > 8 ET < 13 :
« DUP 8 > CL. DUP 13 < CL.»
'RAT STO # Etudiants allant au rattrapage
1: {5 12 13 8 17 2}
VAR RATT
1: {12}
La difficulté est donc principalement de créer le vecteur logique. Pour terminer cette première partie voici un second exemple où l’on veut supprimer les valeurs d’une liste qui ne sont pas entières :
1: { 1 2.5 3.7 8 4}
VAR ENT
1: {1 8 4}
On peut par exemple créer le vecteur logique en testant si le nombre n’est pas plus grand que sa partie entière, ce qui donne :
« DUP DUP IP > NOT CL.» 'ENT STO
La version a priori plus logique : IP == (Est-ce que le nombre est égal à sa partie entière) ne fonctionne pas car la comparaison ne s’effectue plus élément par élément mais entre les listes, le résultat renvoyé est 0 ou 1 et non plus un vecteur logique. Si quelqu’un a une idée, rendez-vous sur le forum de Silicium.
En APL :
ENT ← {(⍵ = ⌊⍵) / ⍵}
ENT 1 2.5 3.7 8 4
Output : 1 8 4