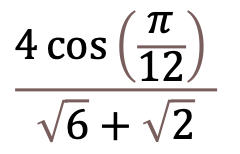Simulateur : https://stendec.io/ctb/rpn_sci.html
Année : 1981 – Prix : 780 Francs en 1983 soit environ 260 EUR
Le « C » de 11C pour préciser que la mémoire est continue (les données ne s’effacent pas en éteignant la machine). Beaucoup de calculatrices étaient à mémoire volatile (comme actuellement la CASIO fx-92), c’est-à-dire que le programme tapé disparait lorsque l’on éteint la machine !
63 lignes de programme + 20 registres jusqu’à 203 lignes et 1 unique registre.
Pile et programme
Nous noterons ENT la touche ENTER.
Quelques manipulations avec la pile à 4 niveaux
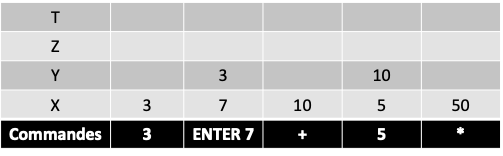
La pile (stack) peut contenir 4 valeurs notées x (l’affichage), y, z et t. Ajouter une valeur x ou appuyer sur ENT décale les autres registres « vers le haut ». Ainsi l’ancien x se retrouve maintenant en y, le y en z, le z en t et le t… est perdu !
Quels résultats obtenez-vous pour chacun de ces calculs ? Expliquez le déroulement
2 ENT 3 * 5 +
...................................................................
2 ENT 3 ENT 5 * +
...................................................................
1 ENT 5 √ + 2 ÷
...................................................................
F FIX 6
...................................................................
0 ENT 1 ENT 2 ENT 3 x ⇆ y
...................................................................Écrivez sur une feuille le contenu de la pile XYZT après cette dernière manipulation.
Sachant que la touche R↓ fait tourner les 4 valeurs de la pile de façon circulaire (t → z → y → x → t), devinez quelles seront les valeurs qui s’afficheront en appuyant plusieurs fois sur R↓.
Se mettre en radians puis trouvez comment calculer :
💻 a regarder chez vous Si vous avez un mac…
Savez-vous que votre MAC possède une calculatrice travaillant en RPN ? Ouvrez le Terminal puis tapez dc (desk calculator). Ce programme existe depuis 1971 et a été créé à l’origine pour les systèmes UNIX par Lorinda Cherry et Robert Morris.
% dc
>>> 2 3 * 5 + f (f permet de voir la pile)
11
>>> 100 k (Travaillons avec 100 décimales, tester avec 1000 !)
>>> c (on efface (clear) le contenu de la pile)
>>> 1 5 v + 2 / f (v pour racine carrée)
1.618033988749894848204586834365638117720309179805762862135448622705\
2604628189024497072072041893911374
Saisir un programme : g P/R
Effacer tout : g P/R puis f PRGM
A gauche le n° du pas 000 – 001 – etc. et à droite le code de la touche tapée, correspondant aux coordonnées physiques (ligne + colonne) sur la machine. Par exemple 15 est le code de la touche 1/x (1ere ligne et 5e colonne).
Que signifient ces 4 codes ?
25
43 26
20
42,21,12
Se déplacer dans le programme : SST (Single STep) et BST (Back STep)
Pour insérer une instruction, par exemple au pas n°14 : Se mettre au pas 13 et tapez l’instruction, le reste du programme se décalera automatiquement.
Pour supprimer une instruction : Se mettre au pas concerné puis touche ←
Sortir de la saisie du programme : g P/R
Revenir au pas n°000 : g RTN
Exécuter un programme en utilisant un label (Etiquette) : LBL suivi d’une lettre entre A et E ou d’un chiffre entre 0 et 9. On peut alors effectuer un branchement inconditionnel (c’est-à-dire sans condition) vers cette étiquette en utilisant GTO (GOTO). Exemple :
g P/R ; f PRGM (Mode programme et effacement)
001 – 42,21,11 LBL A
002 – 1 1
003 – 40 +
004 – 42 31 PSE
005 – 22 11 GTO A
g P/R ; 0 f A pour lancer le programme qui est au label A
R/S : Run / Stop pour lancer ou arrêter un programme.
Exercices
Somme des N premiers entiers
But : Vous entrez un entier N sur la pile puis lancez le programme A, la somme 1+2+…+N = N * (N+1) / 2 s’affiche.
Exemples : 10 f A donne 55 et 5421 f A donne 14 696 331
Lancer d’un dé
f A doit donner un nombre entier entre 1 et 6
Fonctions utiles : RAN#, INT
Pythagore
Comme vous le savez depuis longtemps, dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés. C’est le théorème de Pythagore.
But : L’utilisateur tape 2 valeurs, par exemple 3 ENT 4 et lance le programme A qui lui donne la longueur de l’hypoténuse. Le résultat sera pour l’exemple √(3² + 4²) = 5
Autre exemple : 48 ENT 55 f A doit vous renvoyer 73
Une suite qui converge vers…
On pose u(0) = 0 et u(n+1) = 1 / (1 + u(n))
En partant de 0 à l’affichage, quelle combinaison de touches permet de trouver u(1) puis d’enchainer sur u(2) etc. ? Programmez cette combinaison pour qu’en partant de 0, on voit s’afficher successivement (avec une pause) les premiers termes de cette suite. Lorsque l’affichage sera stabilisé sur une même valeur, appuyez sur R/S pour arrêter. Calculez ensuite l’inverse de ce nombre, le reconnaissez-vous ?
Boucles, tests et mémoires
Repérez les différents tests disponibles à droite de la machine, par exemple x=y. Combien en voyez-vous ?
Lorsqu’un test est VRAI, la machine exécute l’instruction située au pas suivant sinon elle saute ce pas.
g P/R ; f PRGM (Mode programme et effacement)
001 – 42,21,11 LBL A
002 – 42 31 f PSE
003 – 1 1
004 – 30 -
005 – 43 40 g x ≠ 0
006 – 22 11 GTO A Si x ≠ 0 alors retourner au label A
g P/R ; g RTN ; 5 SST SST SST… pour dérouler le programme pas à pas.
On utilise souvent plusieurs sauts et labels dans un même programme pour gérer les différents cas possibles.
Il y a 20 registres (de 0 à 9 et de .0 à .9) avec possibilités d’en ajouter ou d’en enlever pour gagner des pas de programme (nous n’en parlerons pas ici). Que font ces manipulations ?
5 STO 0
4 STO + 0
RCL 0
10 RCL * 0
RCL 0
Exercices
Maximum entre 2 valeurs
But : L’utilisateur saisie 2 valeurs, par exemple 7 ENT 3 et lance le programme. La calculatrice doit afficher 7 car c’est la plus grande des 2 valeurs. Si l’on avait tapé 3 ENT 7, la machine aurait également affiché 7. Écrivez le programme !
Conjecture de Syracuse
La conjecture affirme qu’en partant d’un entier non nul N, on arrivera toujours à 1 en répétant l’algorithme suivant : Si le nombre est pair on le divise par 2 sinon on le multiplie par 3 et on ajoute 1.
Exemples :
N = 5 à 16 à 8 à 4 à 2 à 1. Le maximum est 16 et il aura fallu 5 itérations.
N = 27 à 82 à 41 à 123 à … à 4 à 2 à 1. Le maximum est ?? et il faut ?? itérations.
Il est possible d’écrire un programme en utilisant la pile et aucune des mémoires mais cela demande une bonne connaissance du langage RPN. Vous allez donc créer un programme où le nombre en cours sera enregistré dans le registre n°0, le maximum dans le registre n°1 et le nombre d’itérations dans le registre n°2.
- Par quelles valeurs peut-on initialiser les registres 1 et 2 ?
- Comment tester si un nombre est pair sachant que la machine ne possède pas la fonction modulo mais seulement INT (partie entière) et FRAC (partie décimale) ?
- Comment mettre à jour le maximum ?
- Écrire le programme affichant à la fin le maximum puis le nombre d’itérations avant d’arriver à 1.
- Quel est le maximum et le nombre d’itérations lorsque N = 27 ?
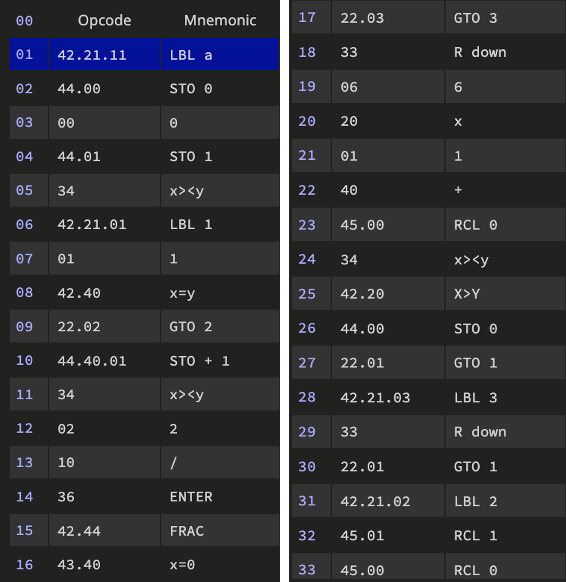
La version ci-dessous n’utilise que 2 registres (maximum dans registre n°0 et nombre d’itérations dans registre n°1)
Remarques :
x >< y est la touche x ⇆ y
R down est la touche R↓
Questions :
Quelles sont les 2 utilisations du 1 que l’on a au pas n°7 ?
Pourquoi y a-t-il un 6 au pas n°19 au lieu d’un 3 ?
A quels pas le maximum est-il mis à jour ?
Un utilisateur tape 3 et lance le programme A :
| T | |||||||||
| Z | |||||||||
| Y | |||||||||
| X | 3 | ||||||||
| Pas | 00 |