Tableaux de fils tendus en Python
Voici quelques exemples de codes en Python pour créer des tableaux de fils, ils sont basés sur des fonctions décrites dans cette vidéo :
Free String Art Boat Pattern
Vous trouverez ici les explications pour créer le tableau à l’ancienne avec de vrais fils et des clous.
Vous pouvez copier-coller le code sur ce site : https://trinket.io/turtle
import turtle
t = turtle.Turtle()
t.speed(0) ; t.hideturtle()
# Ecran avec fond noir
t.color(0,0,0)
t.begin_fill()
for (x,y) in ((-200,200),(200,200),(200,-200),(-200,-200),(-200,200)):
t.goto(x,y)
t.end_fill()
# Représentation des clous
def clou(A):
t.pensize(5) ; t.color((160,140,130))
t.penup(); t.goto(A); t.pendown(); t.goto(A)
# Fil entre le point "A" et le point "B" avec la couleur "c"
# et ajout des clous aux extrémités
def fil(A,B,c):
clou(A) ; t.pensize(1) ; t.pencolor(c) ;
t.goto(B) ; clou(B)
# Division en "n" points du segment entre "a" et "b"
def segment(a,b,n):
return [[(i*PTS[b][0]+(n-1-i)*PTS[a][0])/(n-1), \
(i*PTS[b][1]+(n-1-i)*PTS[a][1])/(n-1)] for i in range(n)]
# Remplissage en utilisant 2 segments S1 et S2
# Chaque point de S1 va vers un point de S2
# puis on revient de S2 vers S1
# sauf si c'est le dernier point
def remplir(S1, S2, c):
for i in range(len(S1)):
fil(S1[i], S2[i], c)
if i < len(S1) - 1 : fil(S2[i], S1[i+1], c)
# Les coordonnées ont été trouvées en utilisant Geogebra
# et l'image fournie en exemple sur le site
PTS = (-142,-100),(0,-110),(2,196),(-62,-122),(142,-116),(-136,-124),
(-122,-152),(142,-124),(126,-164),(-156,-186),(166,-196)
# segment(0,1,40) correspond au segment de (-142,-100) à (0,-110)
# avec 40 divisions
remplir(segment(0,1,40), segment(2,1,40), (180,40,30))
remplir(segment(3,4,40), segment(4,2,40), (240,30,50))
remplir(segment(5,6,20), segment(7,8,20), (120,150,160))
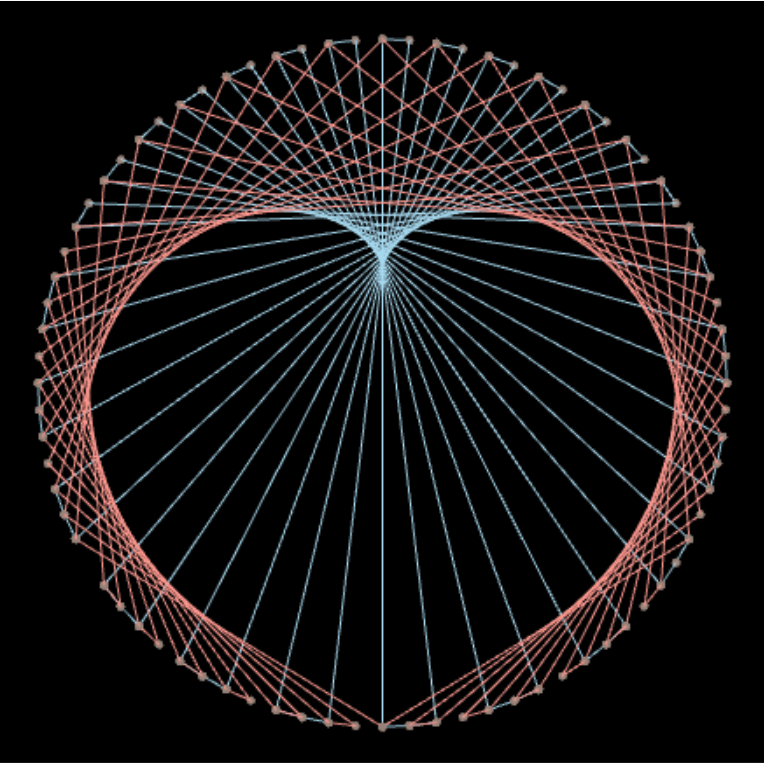
remplir(segment(6,9,10), segment(8,10,10), (0,100,240))Free String Art Heart Circle Pattern
Vous trouverez ici les explications ici. Plus complexe à réaliser !
import turtle
from math import *
t = turtle.Turtle()
t.speed(0) ; t.hideturtle()
t.color(0,0,0)
t.begin_fill()
for (x,y) in ((-200,200),(200,200),(200,-200),(-200,-200),(-200,200)):
t.goto(x,y)
t.end_fill()
def clou(A):
t.pensize(5) ; t.color((160,140,130))
t.penup(); t.goto(A); t.pendown(); t.goto(A)
def fil(A,B,c):
clou(A) ; t.pensize(1) ; t.pencolor(c) ;
t.goto(B) ; clou(B)
# Cercle rayon R divisé en N points
# Position du n-ième clou
def Ce(R,N,n,D=1,d=0):
return [R*sin(2*pi*(n+d/D)/N), R*cos(2*pi*(n+d/D)/N)]
# Partie bleue
c = (175,220,240)
for i in range(14):
fil(Ce(180,80,-14+2*i),Ce(180,80,-13+2*i),c)
fil(Ce(180,80,-13+2*i),Ce(180,80,14+4*i),c)
if i != 13:
fil(Ce(180,80,14+4*i),Ce(180,80,15+4*i),c)
fil(Ce(180,80,15+4*i),Ce(180,80,16+4*i),c)
fil(Ce(180,80,16+4*i),Ce(180,80,-12+2*i),c)
# Partie rose
c = (250,160,150)
pts1 = (40,2),(54,2),(68,4),(14,2),(28,2)
pts2 = (28,2),(29,2),(15,2),(70,4),(55,2),(41,2),(42,2)
for i in range(7):
for j,(a,b) in enumerate(pts1[:-1]):
fil(Ce(180,80,a+b*i),Ce(180,80,pts1[j+1][0]+pts1[j+1][1]*i),c)
if i != 6:
for k,(u,v) in enumerate(pts2[:-1]):
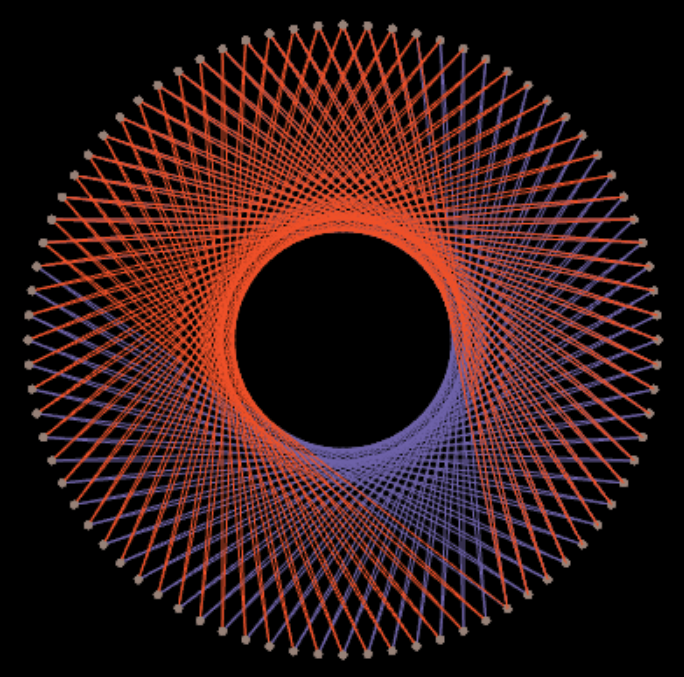
fil(Ce(180,80,u+v*i),Ce(180,80,pts2[k+1][0]+pts2[k+1][1]*i),c)Free String Art Circle 2 Pattern
Vous trouverez ici les explications ici. Assez facile…
import turtle
from math import *
t = turtle.Turtle()
t.speed(0) ; t.hideturtle()
t.color(0,0,0)
t.begin_fill()
for (x,y) in ((-200,200),(200,200),(200,-200),(-200,-200),(-200,200)):
t.goto(x,y)
t.end_fill()
def clou(A):
t.pensize(5) ; t.color((160,140,130))
t.penup(); t.goto(A); t.pendown(); t.goto(A)
def fil(A,B,c):
clou(A) ; t.pensize(1) ; t.pencolor(c) ;
t.goto(B) ; clou(B)
def Ce(R,N,n,D=1,d=0):
return [R*sin(2*pi*(n+d/D)/N), R*cos(2*pi*(n+d/D)/N)]
for (a,b,c) in ((14,63,(120,110,180)),(64,33,(240,90,40))):
for i in range(50):
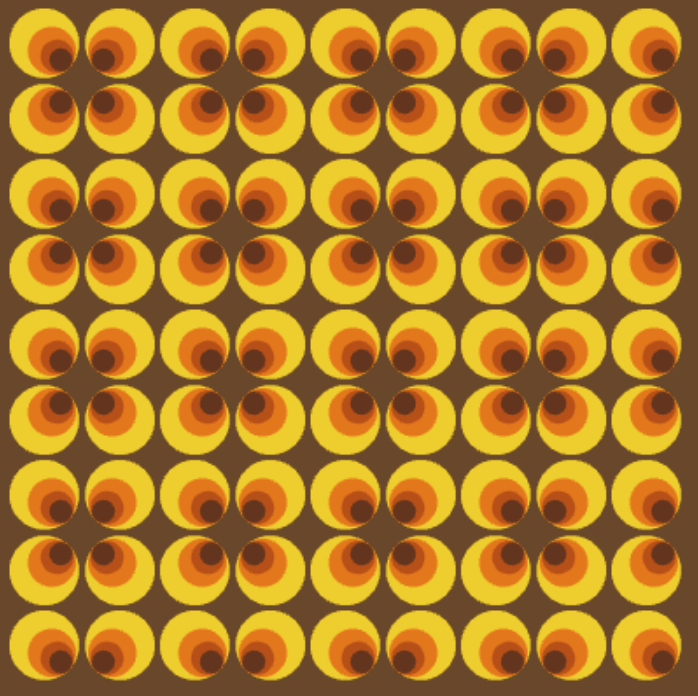
for n in range(2): fil(Ce(180,80,a+i),Ce(180,80,b+i+n),c)Tapisseries des années 70
Voir le programme final en action | Version pour la calculatrice NUMWORKS
import turtle
t = turtle.Turtle()
t.speed(0) ; t.hideturtle()
t.color(115,80,45)
t.begin_fill()
t.goto(0,-400); t.circle(800) # fond marron
t.end_fill()
col, lig, r = 9, 9, 20 # 9*9 motifs de rayon 20
h,e = 4.3*r, .75*r # Calculs des espacements
def motif(x,y,a,r):
t.penup(); t.goto(x,y)
t.setheading(a) # Orientation pour obtenir une des 4 figures
# on parcourt les 4 couleurs
for c in ((240,210,7),(230,130,5),(190,90,14),(110,60,30)):
t.color(c)
t.begin_fill()
t.circle(r,steps=60) # 60 pour un tracé plus précis
r /= 1.45 # Tailles de cercles : jaune, orange, marron...
t.end_fill()
for c in range(col):
for l in range(lig):
a = 45+90*(0,1,3,2)[l%2+2*(c%2)] # angle départ
# Motif à la bonne place et avec la bonne orientation
motif(-160+h*(c//2)+e*(c%2),160-e*(l%2)-h*(l//2),a,r)Répétition de cercles
import turtle
from random import *
from math import sqrt
t = turtle.Turtle()
t.speed(0) ; t.hideturtle()
t.pensize(1)
t.color((220,210,130))
r = 20 # taille des cercles
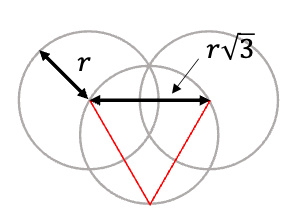
d = sqrt(3) / 2
nc, nl = 400 // r, 280 // r
for c in range(nc):
for l in range(nl):
t.penup()
t.goto(-160 + c * r * d, -140 + l * r - (c % 2) * r / 2)
t.pendown()
t.circle(r)
Fichier pour la TI-83 Premium CE EDITION PYTHON
import turtle
from math import sqrt
t = turtle.Turtle()
t.speed(0) ; t.hideturtle()
h = 20 # taille du motif
p, d = h // 2, sqrt(3) / 2
nb = 1 + int(800 / 3 / h / d)
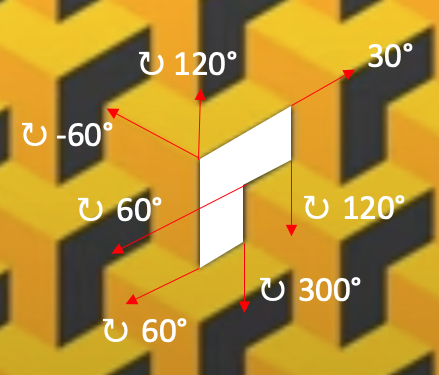
def face(x,y):
t.penup(); t.goto(x,y); t.pendown()
t.setheading(30)
# Chacune des 3 faces a une couleur
for c in ((60,)*3,(230,200,0),(230,165,20)):
t.color(c)
t.begin_fill()
# Dessin d'une face et remplissage
for (u,v) in ((h,120),(p,60),(p,300),(p,60),(p,120),(h,-60)):
t.forward(u)
t.right(v)
t.end_fill()
# On place les motifs
for c in range(nb):
for l in range(nb):
face(-200 + (h + p) * d * c, \
-200 + l * (h + p) - (c % 2) * (h + p) / 2)Lien vers le script pour la calculatrice NUMWORKS
from kandinsky import *
from math import sqrt
from random import randint
# nb d'anneaux (couleurs alternées) et largeur anneau
(nb, r) = (randint(3,40), randint(2,10))
p = nb * r
COUL = (70, 75, 75)
fill_rect(0, 0, 320, 222, (255, 210, 0))
def cercles(u,v,du,dv):
# Bord opposé (en diagonale) au point de départ (u,v)
(u2, v2) = (u + du * nb * r, v + dv * nb * r)
# Pour chaque pixel du carré p * p
for x in range(p):
for y in range(p):
# Recherche du n° de l'anneau
d = int(sqrt(x ** 2 + y ** 2) / r)
# Si c'est un nb impair et qu'il est inférieur au nb d'anneaux total
if d & 1 and d < nb:
# On le dessine (gris foncé)
set_pixel(u + du * x, v + dv * y, COUL)
# Distance point par rapport à l'autre extrémité
# et calcul du n° de l'anneau
d2 = int(sqrt((x - p) ** 2 + (y - p) ** 2) / r)
# On dessine pixel si en dehors des anneaux précédents
if d2 > nb - 2:
set_pixel(u2 - du * x, v2 - dv * y, COUL)
def motif(x,y):
# (a,b) = position départ du motif et (c,d) = directions du remplissage en x et y
# Faire varier (c,d) avec d'autres combinaisons de 1 et -1
for (a,b,c,d) in ((1,1,-1,-1),(2,0,-1,1),(0,2,1,-1),(1,1,1,1)):
cercles(x + a * p, y + b * p, c, d)
for c in range(1+ 160 // p):
for l in range(1 + 110 // p): motif(2 * c * p,2 * l * p)