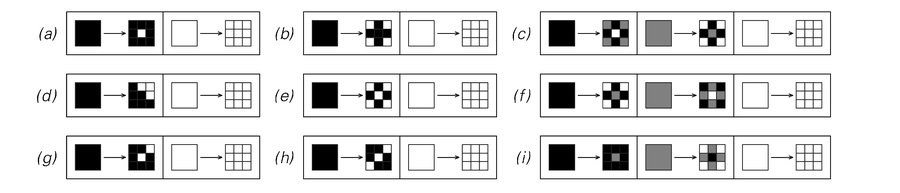
Sur cette page de Wolfram, on peut voir différentes fractales :

Et en bas de cette même page les algorithmes utilisés pour transformer les cases :

Ci-dessous un programme Python qui permet d’appliquer le motif voulu, il suffit d’indiquer les coordonnées des cases blanches. Par exemple pour le (a), la seule case blanche est au milieu (coordonnées (1,1))

from PIL import Image, ImageDraw
import numpy as np

# Dimensions de l'image finale (à modifier comme vous le voulez)
source = Image.new("RGB", (600, 600), color="white")
draw = ImageDraw.Draw(source)

# Recherche s'il y a une case blanche
def has_common(str1, str2, pattern):
    min_len = min(len(str1), len(str2))
    for i in range(1, min_len + 1):
        for p in pattern:
            # Ne pas afficher si on trouve une case blanche
            if str1[-i] == p[0] and str2[-i] == p[1]:
                return False
    # Sinon case noire
    return True

# Construction de la fractale
def fractal(pattern):
    # On parcourt les colonnes
    for c in range(600):
        # Convertir 'c' en base 3 (ici à l'aide de numpy)
        t1 = np.base_repr(c, base=3)
        # On parcourt les lignes
        for l in range(600):
            t2 = np.base_repr(l, base=3)
            # Si pas de case blanche, afficher le point
            if has_common(t1, t2, pattern):
                draw.point((c, l), fill=(0, 0, 0))

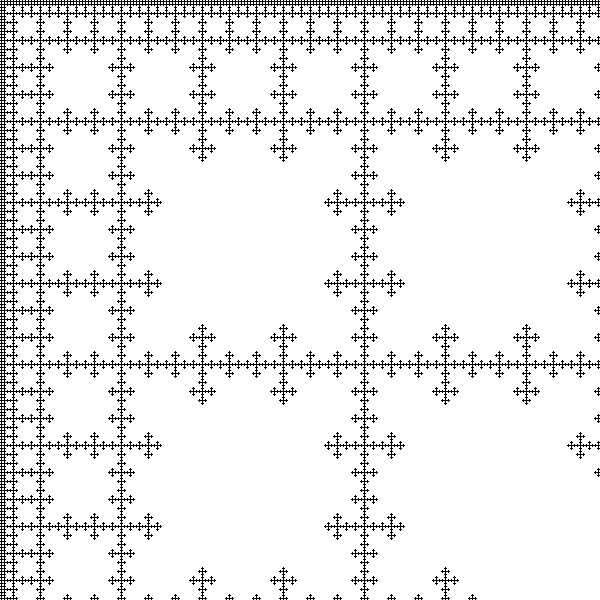
# Exemple avec le tapis de Sierpiński
fractal(["11"])
source.show()

Quelques motifs

Et on peut en inventer de nouveaux :