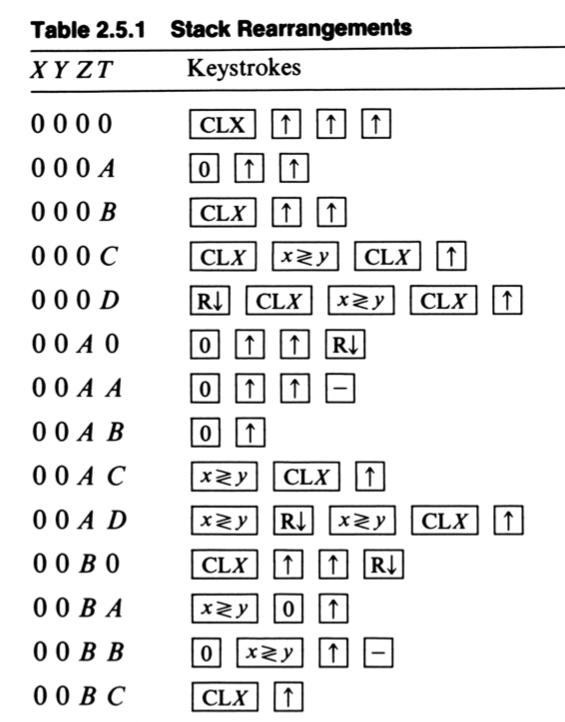
RPN : Recherche de permutations | Index de mes vidéos Youtube

On trouve, dans certains ouvrages sur les calculatrices HP, des tables donnant les combinaisons de touches pour réordonner les éléments de la pile XYZT :

Par exemple ci-dessus, ligne n°9, si ABCD sont sur la pile XYZT, la combinaison x><y, CLX et ENTER permettra d’avoir 00AC sur la pile.

L’idée m’est venue de faire la même chose pour les calculatrices HP-48/49/50g qui ont d’autres commandes pour manipuler la pile.

A partir d’éléments (e1 au niveau 1, e2 au niveau 2 etc.), on voudrait les réordonner en utilisant les commandes de base du langage RPN : DUP, SWAP, DROP, OVER, ROT, DUP2, DROP2 et PICK3.

Exemples :

La pile contient uniquement 2 éléments e1 (niveau 1) et e2 (niveau 2)et on veut les inverser. Réponse : SWAP

La pile contient 3 éléments e1 : e2 : e3 et on veut inverser les éléments des niveaux 2 et 3 pour obtenir e1 : e3 : e2. Réponse : ROT SWAP

Je vous propose un petit programme Python qui fait une recherche brute de toutes les possibilités (en partant des combinaisons à 1 commandes, puis à 2 commandes etc. Avec répétitions, par exemple OVER OVER). Il recherche jusqu’à une combinaison de 7 commandes ce qui peut demander du temps !

Tester le programme en ligne

from itertools import *

keys = "DUP", "SWAP", "DROP", "OVER", "ROT", "DUP2", "DROP2", "PICK3"

def DUP(s): return [s[0]] + s if len(s)>0 else -1
def SWAP(s): return [s[1], s[0]] + s[2:] if len(s) > 1 else -1
def DROP(s): return s[1:] if len(s) > 0 else -1
def OVER(s): return [s[1]] + s if len(s) > 1 else -1
def ROT(s): return [s[2]] + s[:2] +s[3:] if len(s) > 2 else -1
def DUP2(s): return [s[0], s[1]] + s if len(s) > 1 else -1
def DROP2(s): return s[2:] if len(s) > 2 else -1
def PICK3(s): return [s[2]] + s if len(s) > 2 else -1

def find(target, n):
 rr = [1 + v for v in range(n)]
 tr = [int(v) for v in target]
 for n in range(1, 8):
  for op in combinations_with_replacement(keys, n):
   for p in permutations(op):
    r = rr
    for c in p:
     t = eval(c)(r)
     if t == -1: break
     r = t
    if r == tr:
     rs = ':'.join([str(v) for v in rr])
     return '{} -> {} = {}'.format(rs, ':'.join(list(target)), " / ".join(p))

 return "No solution"

# 5 levels on the stack (e1:e2:e3:e4:e5). Goal : e2:e2
>>> find("22", 5)
'1:2:3:4:5 -> 2:2 = ROT / DROP2 / SWAP / ROT / DROP2 / DUP'

# 3 levels on the stack (e1:e2:e3). Goal : e1:e2:e3:e1:e2:e3
>>> find("123123", 3)
'1:2:3 -> 1:2:3:1:2:3 = PICK3 / PICK3 / PICK3'

# 3 levels on the stack. Goal : e1:e1:e2:e2:e3:e3
>>> find("112233", 3)
'1:2:3 -> 1:1:2:2:3:3 = PICK3 / ROT / ROT / DUP2 / ROT'

# 4 levels on the stack. Goal : e2:e2:e4:e4
>>> find("2244", 4)
'1:2:3:4 -> 2:2:4:4 = ROT / DROP2 / DUP2 / ROT'

Version pour la HP-50g

Cette calculatrice a plus de commandes que les HP-48G pour manipuler la pile, j’ajoute DUPDUP, UNROT et 4 ROLL (comme ROT mais avec le niveau 4)

from itertools import *

# Version HP-50g

keys = "DUP", "DUPDUP","SWAP", "DROP", "OVER", "ROT", "UNROT", "DUP2", "DROP2", "PICK3", "_4_ROLL"

def DUP(s): return [s[0]] + s if len(s)>0 else -1
def DUPDUP(s): return [s[0], s[0]] + s if len(s)>0 else -1
def SWAP(s): return [s[1], s[0]] + s[2:] if len(s) > 1 else -1
def DROP(s): return s[1:] if len(s) > 0 else -1
def OVER(s): return [s[1]] + s if len(s) > 1 else -1
def ROT(s): return [s[2]] + s[:2] +s[3:] if len(s) > 2 else -1
def UNROT(s): return s[1:3] + [s[0]] +s[3:] if len(s) > 2 else -1
def DUP2(s): return [s[0], s[1]] + s if len(s) > 1 else -1
def DROP2(s): return s[2:] if len(s) > 2 else -1
def PICK3(s): return [s[2]] + s if len(s) > 2 else -1
def _4_ROLL(s): return [s[3]] + s[:3] +s[4:] if len(s) > 3 else -1

def find(target, n):
 rr = [1 + v for v in range(n)]
 tr = [int(v) for v in target]
 for n in range(1, 8):
  for op in combinations_with_replacement(keys, n):
   for p in permutations(op):
    r = rr
    for c in p:
     t = eval(c)(r)
     if t == -1: break
     r = t
    if r == tr:
     rs = ':'.join([str(v) for v in rr])
     return '{} -> {} = {}'.format(rs, ':'.join(list(target)), " / ".join(p))

 return "No solution"

>>> find("231", 3)
'1:2:3 -> 2:3:1 = UNROT'

>>> find("4123", 4)
'1:2:3:4 -> 4:1:2:3 = _4_ROLL'

>>> find("135", 5)
'1:2:3:4:5 -> 1:3:5 = SWAP / _4_ROLL / DROP2'

>>> find("4321", 4)
'1:2:3:4 -> 4:3:2:1 = SWAP / ROT / _4_ROLL'

Version en PROLOG (en cours de réalisation)

% Règles pour les opérations sur la pile

% SWAP : Inverse les niveaux 1 et 2
swap([A,B|T], [B,A|T]).

% DUP : Duplique le niveau 1
dup([A|T], [A,A|T]).

% DROP : Supprime le niveau 1
drop([_|T], T).

% OVER : Récupère le niveau 2 et le met au niveau 1
over([A,B|T], [B,A,B|T]).

% ROT
rot([A,B,C|T], [C,A,B|T]).


% Règle pour arrêter la récursivité lorsque la pile est déjà dans l'état voulu
trouve([], Stack, Stack).

% Règles pour trouver la séquence d'opérations 

trouve([swap|Actions], Stack, FinalState) :-
    swap(Stack, NewStack),
    trouve(Actions, NewStack, FinalState).

trouve([dup|Actions], Stack, FinalState) :-
    dup(Stack, NewStack),
    trouve(Actions, NewStack, FinalState).

trouve([drop|Actions], Stack, FinalState) :-
    drop(Stack, NewStack),
    trouve(Actions, NewStack, FinalState).

trouve([over|Actions], Stack, FinalState) :-
    over(Stack, NewStack),
    trouve(Actions, NewStack, FinalState).

trouve([rot|Actions], Stack, FinalState) :-
    rot(Stack, NewStack),
    trouve(Actions, NewStack, FinalState).

Quelques tests

rot([1,4,3],X).
Réponse : X = [3, 1, 4]

swap([1,4,3],X).
Réponse : X = [4, 1, 3]

drop([1,4,3],X).
Réponse : X = [4, 3]

over([1,4,3],X).
Réponse : X = [4, 1, 4, 3]

trouve(X, [1,4,3], [4,1,3]).
X = [swap]

Version 2 proposée par chatGPT

trouve(Actions, Stack, FinalState) :-
    trouver_sequence(Actions, [], Stack, FinalState).

% Cas où l'état actuel est l'état voulu
trouver_sequence([], _, Stack, Stack).

% Cas où l'état actuel est différent de l'état voulu, continue à chercher
trouver_sequence([Action|Actions], History, CurrentState, FinalState) :-
    \+ member(CurrentState, History), % Vérifie si l'état actuel a déjà été visité pour éviter les boucles infinies
    apply_action(Action, CurrentState, NextState),
    trouver_sequence(Actions, [CurrentState|History], NextState, FinalState).

% Applique une action sur l'état actuel de la pile
apply_action(swap, [A,B|T], [B,A|T]).
apply_action(dup, [A|T], [A,A|T]).
apply_action(drop, [_|T], T).
apply_action(over, [A,B|T], [B,A,B|T]).
apply_action(rot, [A,B,C|T], [C,A,B|T]).