Yann Le Du m’a fait découvrir via Twitter l’existence du langage K (première version en 1992 !), dont les caractéristiques sont proches de l’APL.

Cette page me servira de mémo pour noter mes découvertes et compréhensions de ce langage (appelé également Shakti). Ce n’est donc pas un cours mais juste des notes personnelles que je partage librement avec vous.

➡ Lien pour tester les codes écrits en K

➡ Références que je vais utiliser : En ligne | PDF

📲 J’ai également une page spéciale consacrée à oK Mobile, une autre version de K.

Quelques challenges Twitter

J’avais proposé sur Twitter (menu Challenges Twitter en haut de ce blog) de résoudre quelques petits exercices en Python, JavaScript ou APL. C’est à cette occasion que Yann Le Du (YLD) a donné ses propres solutions en K. Essayons de décrypter ses réponses !

Isogrammes (Challenge n°3)

Un isogram (En français on parle d’heterogramme) est un mot qui ne contient aucune lettre répétée. Ecrire une fonction qui renvoie vrai ou faux suivant que le mot est un heterogramme, sans tenir compte de la casse (majuscule/minuscule)

Voir les solutions en Python, JS et APL

Solution en K proposé par YLD :

isogram:=/#'?\:_

Le verbe _ permet dans sa version monadique de calculer la partie entière d’un nombre ou de transformer une chaine en minuscules.

 _ 1.5 3.99 -2 -2.1
1 3 -2 -3

 _ "BoNJouR"
"bonjour"

L’opérateur ?, dans sa forme monadique, correspond à l’union (éléments pris de façon unique)

 ? "abracadabra"
"abcdr"

Sous sa forme dyadique, il permet de générer des nombres aléatoires, par exemple tirer 10 nombres aléatoires entre 0 et 2 :

 10 ? 3
2 1 2 2 2 0 1 1 2 0

L’adverbe \: s’appelle “Converge scan” et /: “Converge over”. Les 2 vont répéter les calculs jusqu’à arriver à une convergence (dans le sens : le terme suivant est égal au terme précédent). On peut également imposer le nombre d’itérations :

 {1+1%x}/:1       / u(n+1) = 1 + 1 / u(n) en partant de u(0) = 1
1.618034          / Affichage du résultat final (Nombre d'or)

 (5;{1+1%x})/:1   / 5 itérations uniquement
1.625

 {1+1%x}\:1       / Affichage des résultats intermédiaires
1       
2.      
1.5     
1.666667
1.6     
1.625             / On retrouve la 5e itération
1.615385
1.619048
1.617647
1.618182
...
1.618034

 ?\:"abracadabra"
abracadabra
abcdr

Par contre / (reduce) et scan (\) sont similaires à l’APL :

 +/ 1 2 3 4       / Réduction par la somme
10

 =/ 2 2 1      / 2 = 2 est Vrai puis Vrai = 1 est Vrai
1

 =/ 2 3 0      / 2 = 3 est Faux puis Faux = 0 est Vrai
1

 +\ 1 2 3 4       / Scan par la somme : 1, 1+2, 1+2+3, 1+2+3+4
1 3 6 10

L’adverbe ‘ signifie “pour chaque”, par exemple compter le nombre de lettres de chaque mot :

 #' ("bonjour";"tout";"le";"monde")
7 4 2 5

Signification du code de YLD sur un exemple :

 =/#'?\:_ "moOse"    / moOse est-il un isogram ?
0                    / Réponse = non

Etapes :

 _ "moOse"         / Mettre le mot en minuscules
"moose"

 ?\:_ "moOse"     / Répéter "Union" jusqu'à valeur stable
moose             / Il y aura donc le mot du départ
emos              / et le mot sans doublon

 #'?\:_ "moOse"   / Chercher les tailles des 2 mots
5 4

=/#'?\:_ "moOse"  / Ces tailles sont-elles identiques ?
0                 / si oui c'est un isogram

Gimme (Challenge n°2)

Résumé en français : On vous donne 3 nombres différents dans un ordre quelconque. En sortie, donnez le rang du nombre qui est entre les 2 autres. Par exemple avec 2, 3, 1 c’est le chiffre 2 qui est entre 1 et 3, son rang dans 2, 3, 1 est 0.

Solution proposée par YLD :

 gimme:*1_<

 gimme 5 10 14
1

L’opérateur de tri croissant < fonctionne comme en APL :

 < 14 5 10
1 2 0 

/ Le plus petit nb est à la position 1, c'est le 5
/ Le second nb est à la position 2, c'est le 10
/ Le plus grand est à la position 0, c'est le 14

En version dyadique, _ permet d’enlever des éléments au début ou à la fin d’un tableau :

 2_ 4 5 6 7 8        / On enlève les 2 premiers éléments
6 7 8

 -2_ 4 5 6 7 8       / On enlève les 2 derniers éléments
4 5 6

En version monadique, * récupère le premier élément d’un tableau :

 * 4 5 6 7
4

Signification du code de YLD sur un exemple :

*1_< 8 5 12
0

Etapes :
 < 8 5 12       / Tri du tableau
1 0 2           / L'élément du milieu sera à la position 0

 1_< 8 5 12     / Pour récupérer ce nb on supprime le 1er élément
0 2

 *1_< 8 5 12    / Et on prend le premier élément du tableau
0

Positions des mots (Challenge n°6)

Résumé en français : Vous devez créer un programme qui à partir d’une phrase, met tous les mots distincts dans une liste et retourne une chaine donnant les positions des mots de la phrase initiale dans cette liste. On ne tiendra pas compte de la casse.

Solution proposée par YLD :

,/$'s?s:" "\_

compress:{,/$'s?s:" "\_x}

En version dyadique, \ permet de faire un scan, également de séparer une chaine suivant un caractère (split) mais aussi d’écrire un nombre dans une base quelconque !

 2 +\ 4 5 6
6 11 17        / 2+4, 2+4+5, 2+4+5+6

 ","\ "bonjour,tout,le,monde"        / split avec ','
bonjour
tout   
le     
monde  

 10\ 3574      / Décomposition de 3574 en base 10
3 5 7 4

 2\ 35         / Décomposition de 35 en base 2
1 0 0 0 1 1

Nous avons vu ? en version monadique (Union ou nombres aléatoires), en version dyadique x?y permet de trouver l’index de y dans le tableau x :

 5 7 8 6 ? 7 5  / Positions de 7 et de 5 dans le tableau 5 7 8 6
1 0             / 7 est à la position 1 et 5 à la position 0  

 s:"abcabc"     / affectation de la chaine "abcabc" dans s
 s?s
0 1 2 0 1 2 

$ transforme, en version monadique, un nombre en chaine. L’opération inverse s’effectue via l’opérateur . :

 $ 123      / Transformation d'un nombre en chaine
"123"

 ."123"     / Transformation d'une chaine en nombre
123

 ."2+5"     / Evaluation
7

Signification du code de YLD sur un exemple :

 ,/$'s?s:" "\_ "un deuX un Trois UN deux"
"010301"

Etapes :

 _ "un deuX un Trois UN deux"        / En minuscules
"un deux un trois un deux"      

 " "\_ "un deuX un Trois UN deux"   / Split avec " "
un   
deux 
un   
trois
un   
deux 

 s:" "\_ "un deuX un Trois UN deux"    / Affectation dans s

 s?s:" "\_ "un deuX un Trois UN deux"  / Positions des éléments
0 1 0 3 0 1

 $'s?s:" "\_ "un deuX un Trois UN deux"  / Conversion en chaine
0
1
0
3  
0
1

 ,/ $'s?s:" "\_ "un deuX un Trois UN deux"  / Concaténation
"010301"

Paires de gants (Challenge n°10)

Résumé en français : On vous donne une liste contenant des couleurs de moufles (donc pas de main gauche ou droite à distinguer). On vous demande le nombre de paires que vous pouvez constituer, c’est-à-dire avoir 2 moufles de la même couleur.

Solution proposée par YLD :

 +/\:(0=)_div#'=

Pour grouper les indices d’un tableau à partir des valeurs, on utilise =.

 = 8 5 8 8 5 3      / On groupe les indices à partir des valeurs
3|,5   
5|1 4  
8|0 2 3

 = "abracadabra"
a|0 3 5 7 10
b|1 8       
c|,4        
d|,6        
r|2 9  

Pour obtenir les effectifs de chaque valeur :

 #'= 8 5 8 8 5 3
3|1
5|2
8|3

 #'= "abracadabra"
a|5
b|2
c|1
d|1
r|2

La fonction mathématique div permet d’effectuer une division entière :

 3 div 17     / division entière de 17 par 3
5

 div 17       / division entière par 2
8

Pour filtrer un tableau, on utilise # ou _ :

 notes: 5 12 10 6 19 3     / Notes d'élèves

 (10>)_ notes         / on supprime les notes inférieures à 10
12 10 19

Tableau de symboles :

 s:`red`blue`green
 
 s@1     / élément à la position 1 (ou encore s[1])
`blue

Signification du code de YLD sur un exemple :

 +/\:(0=)_div#'=`red`red`blue`red`blue`green
[blue:1;red:1]
2 

Etapes :

 =`red`red`blue`red`blue`green     / Répartition des indices
blue |2 4  
green|,5   
red  |0 1 3

 #'=`red`red`blue`red`blue`green  / Effectifs
blue |2
green|1
red  |3

 div#'=`red`red`blue`red`blue`green  / Division par 2
blue |1
green|0
red  |1

/ On supprime les restes qui sont nuls 
/ "green" ne permet pas de faire au moins une paire

 (0=)_div#'=`red`red`blue`red`blue`green 
blue|1
red |1

/ On utilise ou non \: pour avoir le détail puis réduction par la somme

 +/(0=)_div#'=`red`red`blue`red`blue`green
2

Explosion (challenge n°12)

Résumé en français : On vous donne une chaine de caractères composée de “chiffres” (‘0’ à ‘9’). Vous devez écrire une fonction qui renvoie une chaine où chaque chiffre est répété le nombre de fois correspondant à sa valeur. Par exemple avec la chaine “312”, on doit répéter 3 fois le “3”, 1 fois le “1” et 2 fois le “2”, ce qui donne la chaine “333122”.

Solution proposée par YLD :

s@&10\. s:

Nous reconnaissons l’affectation s:, la conversion . d’une chaine en numérique, la décomposition d’un nombre en base 10. Il reste à comprendre & et @.

& (where) permet de répliquer les indices d’un tableau autant de fois que les valeurs indiquées dans ce tableau. Exemple :

 & 4 3 0 2           / Répéter 4 fois l'indice 0, 3 fois l'indice 1...
0 0 0 0 1 1 1 3 3

 notes: 5 10 15 9 13 8    / Notes d'élèves

 notes<10        / Positions des élèves n'ayant pas la moyenne
1 0 0 1 0 1

 &notes<10       / Indices correspondants
0 3 5            / Les élèves n°0, 3 et 5 n'ont pas la moyenne

 & 1 0 0 1 1     / Plus généralement, avec un tableau binaire
0 3 4            / on récupère les positions des "1"

x@y donne la valeur qui est à l’indice y du tableau x :

 "sujet"@ 2 1 0 4 3     / Lettres aux positions 2,1,0,4 et 3
"juste"

Signification du code de YLD sur un exemple :

 s@&10\. s:"102269"
"12222666666999999999"

 s:"102269"         / Mémorisation de la chaine dans "s"
 
 . s:"102269"       / Conversion en nombre
102269

 10\. s:"102269"    / Décomposition en base 10
1 0 2 2 6 9 

 &10\. s:"102269"   / On réplique les indices suivant les valeurs
0 2 2 3 3 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5

/ Pour finir on récupère à partir de "s" le caractère à la position 0
/ puis 2 fois celui à la position 2, 2 fois celui à la position 3
/ 6 fois celui à la position 4 et 9 fois celui à la position 5
/ On obtient bien 1,22,22,666666,999999999

Misez p’tit Optimisez en version K

Sur le forum de Silicium, j’avais proposé différentes solutions de challenges (à l’origine pour des calculatrices de poche programmables) en version APL. Je vais en reprendre quelques uns et voir ce que cela peut donner en K.

MPO 9 : Somme des chiffres

Calculer la somme des chiffres d’un nombre.
Par exemple : 352791 doit retourner 27

On a tout ce qu’il faut ! $ pour transformer un nombre en chaine, . pour faire l’inverse, la réduction +/ et ‘ qui signifie “pour chaque” :

 MPO9: +/.'$

 MPO9 352791
27

Tout aussi court, on peut utiliser la décomposition en base 10:

 MPO9: +/10\

 MPO9 352791
27

Si maintenant on veut continuer le processus jusqu’à obtenir un chiffre entre 0 et 9, par exemple :

352791 -> 27 -> 9

Il suffit d’utiliser /: ou \: pour créer la boucle :

 (+/10\)\: 352791       / Affichage des résultats intermédiaires
352791 27 9

 (+/10\)/: 352791       / Uniquement résultat final
9

MPO1 : Evaluation d’un polynôme

Il s’agit d’évaluer le polynôme P(x)=3x^3+4x^2+x+9 en une valeur donnée en paramètre.

Cela revient à convertir le tableau 3 4 1 9 en base x, d’où :

 MPO1: {x/ 3 4 1 9}

 MPO1 7
1241

ovnis

J’avais proposé ce petit exercice pour les calculatrices HP et APL :

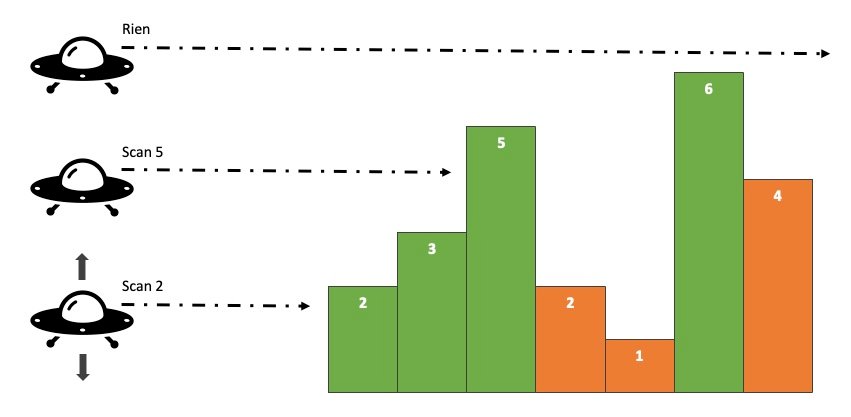
On vous donne une liste de hauteurs d’immeubles adjacents et on vous demande combien seront visibles si vous les regardez à partir de la gauche. Par exemple, si les hauteurs sont 2 3 5 2 1 6 4, en vert ci-dessous les 4 seuls immeubles qui seront visibles (les autres sont cachés par des bâtiments plus hauts)

On supposera dans un premier temps qu’il n’y a pas de zones vides entre les immeubles, c’est-à-dire que la liste ne contient pas de 0 (immeubles de hauteur nulle).

Dans un second temps, considérez le cas général.

Je reprends le corrigé que j’avais mis sur Silicium mais en version K :

On va déjà scanner les immeubles pour récupérer les hauteurs maximales atteintes :

 |\ 2 3 5 2 1 6 4    / On cherche les max progressivement
2 3 5 5 5 6 6

Il faut maintenant récupérer les hauteurs distinctes :

 ?|\ 2 3 5 2 1 6 4
2 3 5 6

Et les compter :

 #?|\ 2 3 5 2 1 6 4
4

Le programme final :

 scan:#?|\

 scan 2 3 5 2 1 6 4
4

Si la liste commence par un ou plusieurs 0, le calcul sera faux :

 scan 0 2 1
2

Ceci parce que les maximums progressifs sont { 0 2 2 } dont la réunion comporte 2 termes {0 2}. Il faut donc filtrer la liste des maximums pour enlever les 0.

 (0=)_ 0 0 2 3 5 5     / Signifie enlever ceux égaux à 0
2 3 5 5

Programme général :

 scan:#?(0=)_|\

 scan 0 0 2 3 5 2 1 6 4
4