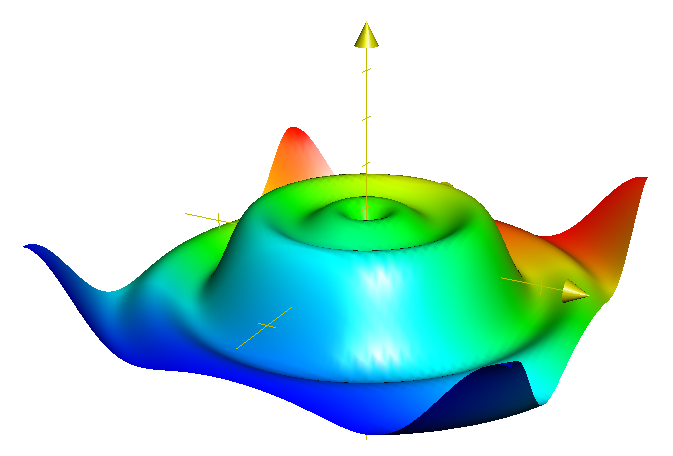
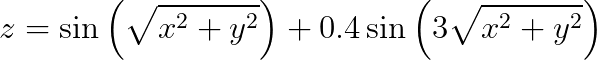Sur d’anciennes revues des années 80, on pouvait voir cette surface 3D ressemblant à un chapeau :

Remarquez que le code du programme (écrit en BASIC) était donné sur la publicité ! Voici à nouveau ce chapeau dans une autre revue :

Passons à sa traduction en Python pour la NUMWORKS :

from math import *
from kandinsky import fill_rect, set_pixel

(BL, WH) = ((0, 0, 0), (255, 180, 50))  # Noir et Orange

fill_rect(0, 0, 320, 222, BL)  # Fond noir

(xp, xr) = (120, 1.5 * pi)
yp = 45
(xf, zf) = (xr / xp, xr / yp)
for zi in range(-yp, yp):
  zt = zi * xp / yp
  xl = int(.5 + sqrt(xp * xp - zt * zt))
  for xi in range(-xl, xl + 1):
    xt = sqrt(xi * xi + zt * zt) * xf
    yy = (sin(xt) + .4 * sin(3 * xt)) * yp
    y1 = int(min(222, max(1, yy - zi + 100)))
    x1 = 10 + int(min(360, max(0, xi + zi + 150)))
    set_pixel(x1, 210 - y1, WH)
    fill_rect(x1, 210 - (y1 - 1), 1, y1, BL)

Equation de la surface

En regardant plus attentivement le code, on voit que les zi (noté y ci-dessous) et xi (noté x) permettent de calculer yy (noté z), l’équation de la surface est :