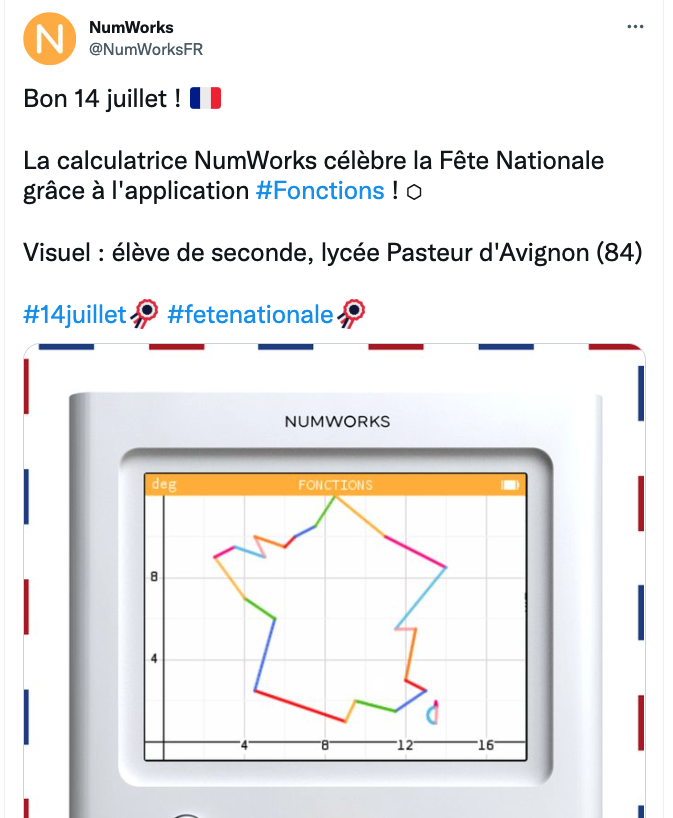
Suite à un Tweet de NumWorks présentant le visuel d’une carte de France, j’ai lancé le challenge de réaliser une carte aussi réaliste que possible (ou faussement réaliste) en Python et en moins de 500 octets.

Retour dans les années 80

Dans les années 80 est sorti un petit ordinateur individuel, le ZX-81. Il n’avait que 1Ko de RAM (soit 1000 caractères) mais permettait de s’initier à la programmation et de créer quelques jeux. L’achat d’une extension 16Ko ou 32Ko était cependant assez rapidement nécessaire.

Voici un programme proposé dans le livre “Pilotez votre ZX 81” de Patrick Gueule :

La machine possédait des caractères semi-graphiques, comme par exemple ◧ ◨. L’astuce dans ce programme est de mémoriser le nombre d’espaces à afficher à partir de la gauche puis le(s) caractère(s) semi-graphique(s), à nouveau le nombre d’espaces ensuite le(s) caractère(s) et terminer par 0 pour passer à la ligne suivante. Ainsi le 7780 de la variable A$ indique qu’il faut afficher 7+7+8=22 espaces et revenir à la ligne (ligne blanche au-dessus de la carte). Ensuite 6+5=11 espaces puis 3 caractères semi-graphiques et retour à la ligne :

Remarquez que les caractères semi-graphiques ayant une dimension de 2×2, cela permet d’afficher 2 rangées de la carte à la fois.

Même idée en Python

Dessinons la carte de France en tapant des 1 dans certaines cellules d’Excel (pour cela importez une image de la France dans Mise en Page – Arrière Plan, sélectionnez toutes les cellules puis Accueil – Mise en forme conditionnelle – Règle de surlignage – Egal à 1 – Mettre une couleur de remplissage).

A côté de la carte tapez la formule =A1+2*B1+4*A2+8*B2. Cela permet de convertir les 4 cellules (jaune sur la carte) en un nombre entre 1 et 1+2+4+8=15.

On peut alors étendre cette formule horizontalement et verticalement pour recouvrir toute la carte.

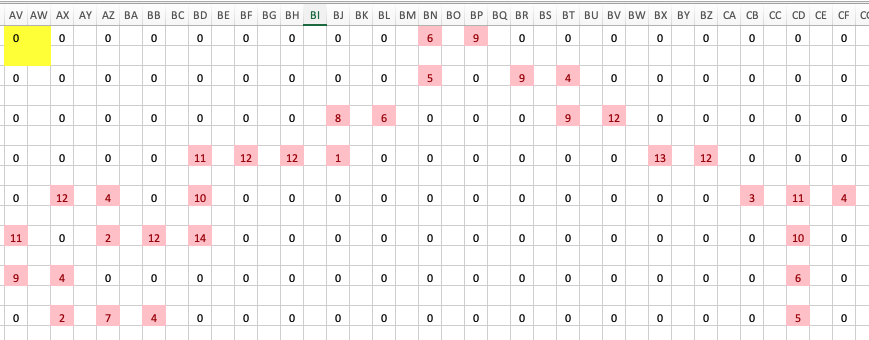
Si on écrit le 9 de la première ligne en binaire :

> bin(9)
'0b1001'

Cela signifie que les cellules 1 et 4 contiennent un 1 et les autres un 0. Il s’agit du caractère ci-dessous :

On est alors dans la même configuration que sur le ZX-81, on doit compter le nombre d’espaces (les 0) puis un caractère graphique codé sur 4 cases.

Voici le début du codage :

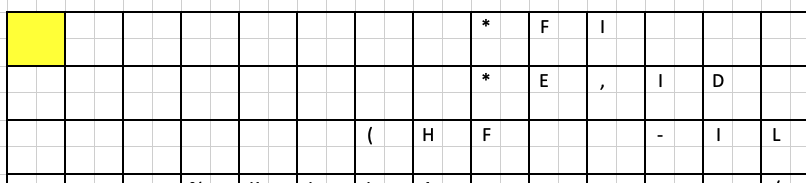
Les lettres F et I de la première ligne sont simplement les 6e et 9e lettres de l’alphabet et permettent donc de coder les nombres 6 et 9.

Le caractère * a 42 comme code Ascii, notre référence étant le code 33, ce qui fait une différence de 9 soit 9 espaces.

> ord('*')
42
> chr(33)
'!'

Enfin, j’utiliserai le caractère ‘!’ pour les fins de ligne. Le contour de la carte peut donc être traduit par :

FR = '*FI!*E,ID!(...'

Pour le programme principal, il suffit, suivant le code Ascii, de décider si l’on doit revenir à la ligne (caractère ‘!’ de code 33), se décaler suivant l’axe des x d’un certain nombre d’espaces ou afficher un caractère semi-graphique :

x, y = 0, 0
for s in FR:
 n = ord(s)
 if n == 33: x, y = 0, y + 10        # Retour à la ligne
 elif n < 55: x = 10 * (n - 33)      # 10 pixels par "espace"
 else: 
  car(n - 64)   # Affichage du caractère semi-graphique
  x += 10       # Et décalage à droite de 10 pixels

Pour la fonction car, soit on décompose le paramètre en binaire pour savoir quelles cases on doit remplir, soit on les récupère petit à petit. Par exemple, si le caractère semi-graphique est L :

> ord('L')      # on récupère son code Ascii
76
> 76 - 64       
12              # 12e lettre
> bin(12)       
'0b1100'    # 2 premières cases noires et suivantes blanches
> 12 >> 0 & 1   # On peut aussi récupérer 1-1-0-0 petit à petit 
0
> 12 >> 1 & 1
0
> 12 >> 2 & 1
1
> 12 >> 3 & 1
1

Fonction car avec des carrés noirs de 5*5 pixels :

def car(x, y, n):
 for i in range(4):
  if n >> i & 1:
   fill_rect(x + i % 2 * 5, y + i // 2 * 5, 5, 5, (0,0,0))

Programme final ici

Avec la tortue

Une autre idée est de parcourir le contour de la carte avec la tortue. Pour rester dans les 500 octets imposés, il ne faudra utiliser que quelques points stratégiques.

Pour cela on peut ouvrir la carte de France dans Gimp et utiliser l’outil Chemin :

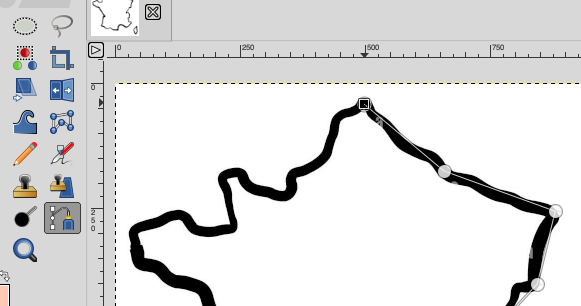
On note les coordonnées des points dans un tableur. L’idée est de partir d’un des points du contour puis de déplacer la tortue en utilisant uniquement les différences entre les coordonnées :

Par exemple, pour passer du point (64,58) au point (62, 61) on se décale du vecteur (-2,3). L’intérêt ? On utilisera moins de caractères pour mémoriser les coordonnées !

Voici le codage de la carte, sachant que le point initial est en (90,-60) qui correspond au nord de la Corse

F = '18!23!3!30...'

Déplacer la tortue du vecteur (1,8) puis (-2,3) puis (-3,-30) etc.

Ce qui donne cette version :

from turtle import *

F = '18!23!3!30!53!11!2!8!5!55!32!9!3!5305!40!6!3!8!1!3!33!D22!2!5!4!6!1!4!4!3!4!1!2!12!1!2!10!28!11260!2!720124!12!25!11!73098E5!29!66043!223!1B51'

def f(s = 1): 
 global i
 if F[i] == '!': i, s = i + 1, -1
 i += 1
 return s * int(F[i - 1], 16)

x = y = i = 0
penup()
while i < len(F):
 goto(90 + 3 * x, -60 - 3 * y)
 pendown()
 x += f()
 y += f()
hideturtle()

Mais le résultat n’est pas très joli car trop rectiligne et la Corse est reliée à la métropole

On va ajouter de l’aléatoire en faisant varier la trajectoire entre 2 coordonnées. Pour cela on doit décomposer le segment (x1,y1) vers (x2,y2) en sous-segments :

for j in range(9):   # Décomposition en 9 étapes...
  goto(90 + g(u,x,j),-60 - g(v,y,j))  # ...entre (u,v) et (x,y)

def g(a, b, j): return 3 * (a + (b - a) * j / 9)   # Interpolation

Et avec de l’aléatoire :

def g(a,b,j): return 3 * a + 2 * random() + (b - a) * j / 3

Concernant la séparation avec la Corse, l’astuce utilisée est qu’avec la NumWorks pensize(0) ne trace pas de trait. Ainsi en ajoutant :

pensize(not(18 < i < 23))

On aura un trait d’épaisseur 1 sauf si i est entre 18 et 23 qui correspond au trait reliant la Corse.

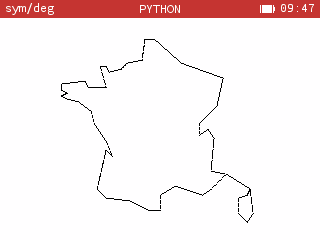
Enfin, on peut dessiner de petits cercles à chaque étapes plutôt qu’un trait simple, on obtient finalement ce script qui fait exactement 500 octets avec le résultat suivant :