Résumé en français : On vous donne une matrice carrée et un nombre n, vous devez renvoyer cette matrice dont les tous les termes ont été tournés (n rotations) dans le sens anti-horaire. Exemple avec une matrice 3 x 3 :
Matrice initiale
1 2 3
4 5 6
7 8 9
n = 1 rotation anti-horaire
3 6 9
2 5 8
1 4 7
n = 2 rotations anti-horaire
9 8 7
6 5 4
3 2 1
n = 3 rotations anti-horaire
7 4 1
8 5 2
9 6 3Python : Facile avec une bibliothèque
La méthode rot90 de la bibliothèque Python numpy permet d’effectuer des rotations de tableaux :
>> import numpy as np
>> np.rot90([[1, 2], [3, 4]], 1) # 1 rotation anti-horaire
array([[2, 4],
[1, 3]])
>> np.rot90([[1, 2, 3], [4, 5, 6]], 2) # 2 rotations, matrice 2 x 3
array([[6, 5, 4],
[3, 2, 1]])Remarquons que 2 rotations n1 et n2 sont équivalentes si la différence n1 – n2 est un multiple de 4. Par exemple, effectuer 1 rotation anti-horaire est équivalent à faire 5 rotations anti-horaires.
De façon plus générale, n rotations anti-horaires sont équivalentes à n % 4 rotations anti-horaires. D’où cette version finale en Python :
import numpy as np
def rotation(matrice, n):
return np.rot90(matrice, n % 4).tolist()
>> rotation([[1, 2], [4, 5]], 2)
[[5, 4], [2, 1]]JavaScript & APL : Effort moyen avec renversements et transposée
Renversements et transposée
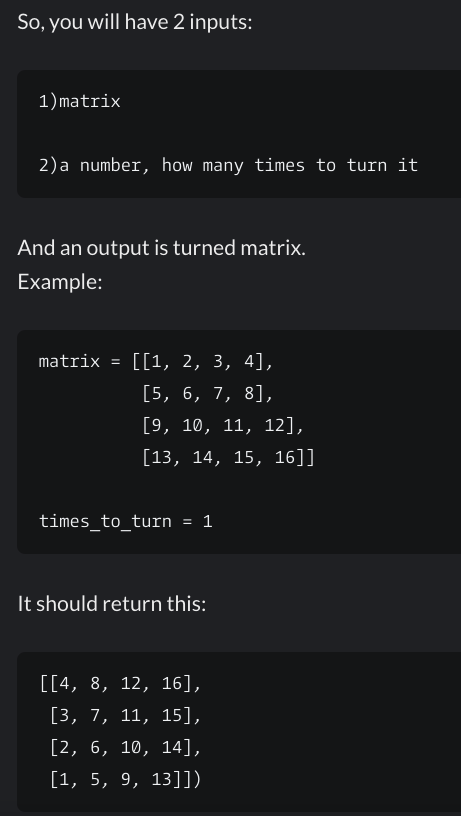
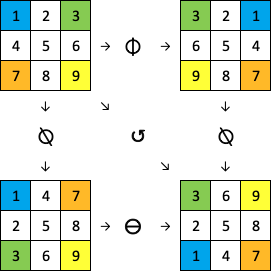
Le diagramme ci-dessous montre que l’on peut obtenir une rotation anti-horaire ↺ à l’aide de ⍉ (transposée) et ⊖ (renversement vertical) ou de ⍉ et ⌽ (renversement horizontal) :
APL
APL dispose de plusieurs primitives pour effectuer des renversements et transposée :
m ← 2 2 ⍴ ⍳4 ⍝ Matrice 2 x 2
m
1 2
3 4
⌽ m ⍝ renversement horizontal
2 1
4 3
⊖ m ⍝ renversement vertical
3 4
1 2
⍉ m ⍝ transposée
1 3
2 4Vérifions :
m ← 3 3 ⍴ ⍳9
m
1 2 3
4 5 6
7 8 9
(⊖⍉) m
3 6 9
2 5 8
1 4 7
(⍉⌽) m
3 6 9
2 5 8
1 4 7Nous avons vu dans l’exercice n°9 que ⍣ permet de répéter une opération plusieurs fois, par exemple pour 4 rotations anti-horaires (ce qui redonnera bien sûr la matrice initiale) :
((⊖⍉) ⍣ 4) m
1 2 3
4 5 6
7 8 9D’où cette version finale en APL :
rotation ← { (⍉⌽) ⍣ (4|⍺) ⊢ ⍵ }
3 rotation 3 3 ⍴ ⍳9
7 4 1
8 5 2
9 6 3
1 rotation 4 4 ⍴ ⍳16
4 8 12 16
3 7 11 15
2 6 10 14
1 5 9 13Javascript
La bibliothèque JavaScript Ramda permet également de faire des renversements et de transposer des tableaux. On peut donc comme en APL remplacer la rotation anti-horaire par la combinaison transpose et reverse. Exemple que vous pouvez tester ici :
R.transpose([[1, 2], [3, 4]]).reverse()
[[2, 4], [1, 3]]Version finale récursive à tester ici :
var rotation = (matrice, n) => {
n %= 4 // reste division par 4
if (n == 0) return matrice // fin récursivité
matrice = R.transpose(matrice).reverse() // rotation anti-horaire
return rotation(matrice, n - 1) // appel récursif
}
>> rotation([[1, 2], [3, 4]], 1)
[[2, 4], [1, 3]]JavaScript & Python : Version sans bibliothèque
Pour se fixer les idées, supposons que l’on ait une matrice 3 x 3. Observez que faire une rotation anti-horaire, c’est remplacer la 1ere ligne par la dernière colonne, la 2e ligne par la 2e colonne et la 3e ligne par la 1ere colonne :
matrice initiale
1 2 3
4 5 6
7 8 9
rotation anti-horaire
3 6 9 // 1ere ligne = 3e colonne de la matrice initiale
2 5 8 // 2e ligne = 2e colonne de la matrice initiale
1 4 7 // 3e ligne = 3e colonne de la matrice initialeDit autrement, faire une rotation anti-horaire, c’est prendre les colonnes de la droite vers la gauche et les écrire en lignes.
Ce que l’on peut traduire en Python ou JavaScript par :
anti_horaire = matrice => {
res = [ ]; // Matrice finale
taille = matrice.length; // Taille matrice
for (l = 0; l < taille; l++) { // Création de chaque ligne
ligne = [ ]; // Initialisation
for (i = 0; i < taille; i++) { // Chaque élément de la ligne
ligne.push(matrice[i][taille - l - 1])
};
res.push(ligne) // Ajout de la ligne
};
return res; // On retourne le résultat
}
>> anti_horaire([[1,2,3], [4,5,6], [7,8,9]])
[3, 6, 9]
[2, 5, 8]
[1, 4, 7]javascript
Comme il s’agit de transformer chacune des lignes, on peut également utiliser map. Voici ci-dessous la même version du programme précédent. Le matrice[0] permet de récupérer la première ligne de la matrice et donc un tableau qui a la largeur de cette matrice, son contenu ne nous intéresse pas puisqu’il va être calculé, d’où le _. Pour chaque numéro de ligne (variable l), on remplace les éléments par la colonne correspondante en partant de la droite (x.length – l – 1):
anti_horaire = matrice =>
matrice[0].map((_,l) => matrice.map(x => x[x.length - l - 1]))Version finale (sans bibliothèque) en JavaScript :
const rotation = (matrice, n) => {
for (i = 0; i < n % 4; i++)
matrice = matrice[0].map((_,l) =>
matrice.map(x => x[x.length - l - 1]))
return matrice
}
>> rotation([[1,2,3], [4,5,6], [7,8,9]], 1)
[3, 6, 9]
[2, 5, 8]
[1, 4, 7]
>> rotation([[1,2,3], [4,5,6], [7,8,9]], 2)
[9, 8, 7]
[6, 5, 4]
[3, 2, 1]Python
Comme nous l’avons vu, faire une rotation anti-horaire, c’est faire une transposée (remplacer la 1ere ligne par la 1ere colonne, la 2e ligne par la 2e colonne etc.) puis inverser l’ordre des lignes :
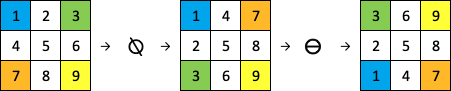
Voici comment inverser les lignes en Python :
>> [[1, 2, 3], [4, 5, 6], [7, 8, 9]] [::-1]
[[7, 8, 9], [4, 5, 6], [1, 2, 3]]Ce qui donne ce programme final :
def rotation(matrice, n):
for _ in range(n % 4):
matrice = [[r[i] for r in matrice] for i in range(len(matrice))][::-1]
return matriceOu cette autre version avancée qui utilise la notion de dépaquetage avec zip et * :
def rotation(matrice, n):
for _ in range(n % 4):
matrice = [list(col) for col in list(zip(*matrice))][::-1]
return matriceQuelques exemples pour mieux comprendre zip et * :
>> [* [[1, 2], [3, 4]]] # Exemple n°1 de dépaquetage
[[1, 2], [3, 4]]
>> [* {1, 2, 3}] # Exemple n°2 de dépaquetage
[1, 2, 3]
>> [* 'abcd'] # Exemple n°3 de dépaquetage
['a', 'b', 'c', 'd']
>> list(zip([1,2], [3,4]))
[(1, 3), (2, 4)]
>> list(zip([[1, 2], [3, 4]])) # ne fonctionne pas
[([1, 2],), ([3, 4],)]
>> list(zip(* [[1, 2], [3, 4]])) # Il faut déjà dépaqueter
[(1, 3), (2, 4)]