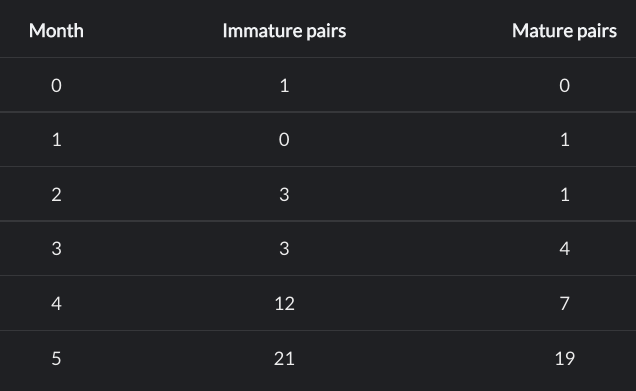
Résumé en français : Des lapins naissent et deviennent matures au bout de 1 mois, âge auquel ils pourront se reproduire.
Créez une fonction qui détermine le nombre de paires de lapins matures après n mois en commençant par un unique couple de lapins immatures et qui se reproduisent à raison de b paires à la fin de chaque mois. Voir le tableau ci-dessus dans le cas de n = 5 mois avec un taux de reproduction de b = 3 pour bien comprendre le déroulement. Quelques autres exemples :

>> lapins(0, 4)
0                     # Après 0 mois, il n'y a pas de paire adultes
>> lapins(1, 4)
1                     # Après 1 mois, une seule paire d'adultes
>>lapins(4, 0)
1                     # Lapins stériles (taux = 0), on reste à 1
>> lapins(6, 3)       
40 
>> lapins(8, 12)
8425
>> lapins(7, 4)
181 

# (1 0) > (0 1) > (4 1) > (4 5) > (20 9) > (36 29) > (116 65) > 181

Cet exercice étant assez facile, proposons différentes versions :

Une simple boucle

On part de 0 adulte et d’une paire de lapins immatures. Chaque mois, le nouveau nombre d’immatures est égal au nombre d’adultes qui se reproduisent avec un taux b (c’est-à-dire la multiplication du nombre d’adultes par le coefficient b). Et le nouveau nombre d’adultes est égal au nombre d’adultes précédents + les immatures précédents qui deviennent adultes.

Il faut faire attention à l’écriture du processus, voici une version INCORRECTE :

def lapins(n, b):
    immatures, adultes = 1, 0
    for i in range(n):
        immatures = b * adultes         # on écrase immatures trop tôt
        adultes =  adultes + immatures
    return adultes

En effet, on commence par mettre à jour la variable immatures puis on utilise cette valeur à la ligne suivante, or nous avions besoin de la valeur précédente de immatures et non pas de la valeur actualisée. Une technique classique est d’utiliser une variable temporaire :

def lapins(n, b):
    immatures, adultes = 1, 0
    for i in range(n):
        temp = immatures            # On mémorise valeur précédente
        immatures = b * adultes
        adultes =  adultes + temp   # que l'on utilise ici
    return adultes

Mais en Python ou en JavaScript, on peut également utiliser cette écriture CORRECTE :

python

def lapins(n, b):
    immatures, adultes = 1, 0
    for i in range(n):
        immatures, adultes = b * adultes, adultes + immatures
    return adultes

>> lapins(8,12)
8425
>> lapins(0,4)
0
>> lapins(4,0)
1

javascript

La traduction est quasi identique en JavaScript :

 const lapins = (n, b) => {
  let [immatures, adultes] = [1, 0];
  for (let i = 0; i < n; i++) {
    [immatures, adultes] = [adultes * b, immatures + adultes];
  }
  return adultes;
}

Avec d’infinies variations, par exemple en utilisant un objet et une boucle Tant que :

const lapins = (n, b) => {
  const tous = {immatures: 1, adultes: 0};    // Tous les lapins
  mois = 0;
  while (mois < n) {
    let temp = tous.adultes;
    tous.adultes += tous.immatures;
    tous.immatures = temp * b;
    mois++;
  }  
  return tous.adultes;
}

Version récursive

Reprenons l’exemple proposé dans l’énoncé avec n = 5 et b = 3. Le nombre de paires d’adultes matures est successivement : 0 → 1 → 1 → 4 → 7 → 19

Si on note u la suite donnant le nombre d’adultes au fil des mois, on a u(0) = 0, u(1) = 1 etc.

Cette suite peut être définie par une relation de récurrence :

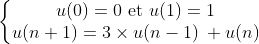
Ce qui signifie que le nombre de paires d’adultes au mois n+1 est 3 fois le nombre de paires d’adultes 2 mois avant (reproduction) + les immatures du mois précédent qui deviennent adultes.

Essayez en effet de vous convaincre que 0 → 1 → 1 → 4 → 7 → 19 correspond à :

u(2) = 1 = 3 * 0 + 1, u(3) = 4 = 3 * 1 + 1, u(4) = 7 = 3 * 1 + 4, u(5) = 19 = 3 * 4 + 7 🤔

Les traductions en Python et JavaScript sont immédiates :

Python

def lapins(n, b):
  if n <= 1: return n
  return b * lapins(n - 2, b) + lapins(n - 1, b)

JavaScript

const lapins = (n, b) => n <= 1 ? 
                         n : 
                         b * lapins(n - 2, b) + lapins(n - 1, b)

>> lapins(5,3)
19
>> lapins(8,12)
8425

Version matricielle

Autre vision en utilisant cette fois-ci un calcul matriciel. En effet, observons que :

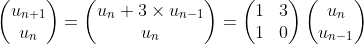
On peut donc calculer u(n+1) et u(n) à l’aide des puissances d’une unique matrice 2 x 2 :

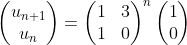
De façon plus générale, le nombre de paires d’adultes pour un taux de reproduction b peut être calculé par :

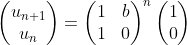
Python

Pour calculer la puissance d’une matrice 2 x 2, nous pouvons créer une fonction de multiplication ou utiliser une bibliothèque comme numpy :

import numpy as np                 # On importe numpy

m = np.array([[1, 3], [1, 0]])     # Création de la matrice m

for k in range(5):                 # Calcul de m^0, m^1... m^4
  print('m^{} = {}'.format(k, np.linalg.matrix_power(m, k)))

Résultats

m^0 = [[1 0], [0 1]]
m^1 = [[1 3], [1 0]]
m^2 = [[4 3], [1 3]]
m^3 = [[ 7 12], [ 4  3]]
m^4 = [[19 21], [ 7 12]]

Attention cependant, la bibliothèque numpy ne gère pas (par défaut) les entiers arbitrairement grands et peut donner des résultats FAUX :

>> np.linalg.matrix_power(m, 50)      # m à la puissance 50

[[ 827677709047869124 1078278355240672323]
 [ 359426118413557441  468251590634311683]]    # Résultat EXACT

>> np.linalg.matrix_power(m, 70)      # m à la puissance 70
[[   23110438186405259  6654818438609454037]
 [-3930641878366699193  3953752316553104452]]  # Résultat FAUX !

On peut malgré tout préciser comment les données doivent être stockées (entier, flottant, objet) :

import numpy as np

m = np.array([[1, 3], [1, 0]], dtype=object)  # en tant qu'objet

>> np.linalg.matrix_power(m, 70)
[[14551031556125490725277067 18956729415189764489429973]
 [6318909805063254829809991 8232121751062235895467076]]   # EXACT !

Programme final en Python :

import numpy as np

def lapins(n, b):
    m = np.array([[1, b], [1, 0]], dtype=object)
    return np.linalg.matrix_power(m, n)[1][0]    # on récupère u(n)

>> lapins(8, 12)
8425
>> lapins(0, 4)
0
>> lapins(4, 0)
1

Javascript

Il existe des bibliothèques JavaScript pour faire du calcul matriciel, par exemple math.js :

>> m = [[1, 3], [1, 0]]

>> math.pow(m,4)
0: [19, 21]
1: [7, 12]

>> math.pow(m,70)
0: [1.455103155612549e+25, 1.8956729415189765e+25]
1: [6.318909805063255e+24, 8.232121751062236e+24]

Sinon, vous pouvez vous créer une petite fonction permettant de mettre une matrice 2 x 2 à une puissance quelconque, par exemple :

const power = (m, n) =>      // Matrice m à la puissance n
{
    [[a, b], [c, d]] = m;    // On récupère les coefficients
    r = [[1, 0], [0, 1]]     // Matrice unité
    for (i = 0; i < n; i++)  // n multiplications matricielles
    {
      [e, f] = [a * r[0][0] + c * r[0][1], b * r[0][0] + d * r[0][1]];
      [g, h] = [a * r[1][0] + c * r[1][1], b * r[1][0] + d * r[1][1]];
      r = [[e, f], [g, h]];
    };
    return r
}

>> power([[1, 3],[1, 0]], 4)
0: [19, 21]
1: [7, 12]

>> power([[1, 3],[1, 0]], 70)
0: [1.455103155612549e+25, 1.8956729415189765e+25]
1: [6.318909805063255e+24, 8.232121751062236e+24]

Programme final en JavaScript qui utilise la fonction power ci-dessus :

lapins = (n, b) =>  power([[1, b],[1, 0]], n)[1][0]

>> lapins(8, 12)
8425

Version APL

Reprenons l’idée du calcul matriciel. En APL, on définit une matrice en précisant ses dimensions suivi de ⍴ et des valeurs :

      m ← 2 2 ⍴ 1 3 1 0     ⍝  Matrice 2 x 2
1 3
1 0

Pour la mettre au carré on utilise le produit interne (ici somme des produits) :

      m +.× m
4 3
1 3

Et avec une réduction on peut obtenir par exemple m^4 :

      +.×/ m m m m
┌─────┐
│19 21│
│ 7 12│
└─────┘

Pour généraliser à une puissance quelconque r, il va falloir dupliquer la matrice r fois, exemple avec r = 4 :

      4 ⍴ ⊂ m
┌───┬───┬───┬───┐
│1 3│1 3│1 3│1 3│
│1 0│1 0│1 0│1 0│
└───┴───┴───┴───┘

D’où cette fonction pour mettre une matrice m à la puissance r :

      power ← {+.×/ ⍺ ⍴ ⊂ ⍵}

      4 power m
┌─────┐
│19 21│
│ 7 12│
└─────┘
      1 power m
┌───┐
│1 3│
│1 0│
└───┘
      0 power m
DOMAIN ERROR

Cette alternative suggérée par Dyalog APL sur Twitter a l’avantage de gérer le cas r = 0 :

      power ← {+.× ⍣ (⍺ - 1) ⍨ ⍵}

      4 power m
19 21
 7 12
      1 power m
1 3
1 0
      0 power m      ⍝ On obtient bien la matrice identité
1 0
0 1

⍣ permet de répéter une opération plusieurs fois et ⍨ d’inverser les paramètres :

      ×⍣3 ⍨ 2       ⍝ 2 → 2 × 2 = 4 → 4 × 4 = 16
16
      +⍣3 ⍨ 2       ⍝ 2 → 2 + 2 = 4 → 4 + 4 = 8
8
      +∘÷⍣ 20 ⍨1    ⍝ 1 + 1 / (1 + 1 / (1 + ...)) ≃ Nombre d'or
1.618033985

Une fois que l’on aura calculé la puissance de la matrice, il faut récupérer l’élément à la ligne 2 et colonne 1. Pour cela, on utilise ⊃ (pick) et on accole (laminate) les lignes de la matrice :

      m ← 2 2  ⍴ 7 9 5 8     ⍝ Matrice 2 x 2
      ,/ m                   ⍝ Laminage (on accole les lignes)
┌───┬───┐
│7 9│5 8│
└───┴───┘
      2 ⊃ ,/ m               ⍝ 2e terme
5 8
      2 1 ⊃ ,/ m             ⍝ 1er terme du 2e terme
5

⍝ On peut également utiliser ⌷ (index)

      2 1 ⌷ m
5

Programme final en APL :

      lapins ←  {2 1 ⌷ +.× ⍣ (⍺ - 1) ⍨ 2 2 ⍴ 1 ⍵ 1 0} 

      8 lapins 12
8425
      0 lapins 4
0
      4 lapins 0
1
      7 lapins 4
181